Question

Figure shows an elevator cabin, which is moving downwards with constant acceleration a. A particle is projected from corner A, directly towards diagonally opposite corner C, then prove that:

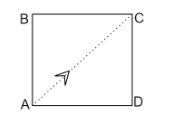
(A) Particle will hit C only when $a = g$
(B) Particle will hit wall CD if $a < g$
(C) Particle will hit the roof BC if a>g

Answer 1

Hint
Every object on earth tends to fall towards the ground. So whenever it is thrown upwards with any velocity it always experiences a downward force that is equal to g and makes it follow a projectile path. But when the reference (elevator cabin here) itself is accelerating, both of these quantities add up and give a net direction of acceleration, which the object thrown inside the elevator would also experience.

Complete step by step answer
An accelerating elevator cabin is a non-inertial frame of reference, it is accelerating. This acceleration causes the object to feel a force and to follow a path that is not a straight line, even if it is thrown with a constant velocity and a fixed direction.
We keep the elevator cabin as the frame of reference, as it is non-inertial, and would appear as a pseudo force which acts in the upward direction. We take upwards as positive direction then-
Case (a): When $a = g$ :

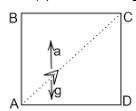
The directions of g and a are opposite, so the relative acceleration of the object is given by:
${a_{net}} = \vec g + \vec a$
${a_{net}} = a - g$
${a_{net}} = g - g = 0$
The object experiences no external force and moves with the constant velocity with which it was projected. It reaches C.
Case (b): When $a < g$

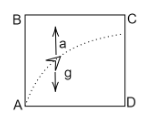
${a_{net}} = \vec g + \vec a$
${a_{net}} = a - g < 0$
Therefore the object experiences a net downward force, which causes it to follow a projectile motion, due to which it hits the surface CD.
Case (c): When $a > g$

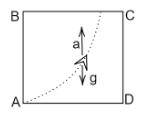
${a_{net}} = \vec g + \vec a$
${a_{net}} = a - g > 0$
Therefore the object experiences a net upwards force, so it follows a projectile motion with upward acceleration, so it hits the roof.

Note
The object is freely falling at all times, or if viewed from an inertial frame of reference, the object only moves with a velocity with which it is projected and follows a projectile path as it would normally do on earth. It is the elevator cabin that accelerates at different rates, which allows the object to either hit C, CD, or the roof. When we take the elevator as a non-inertial frame of reference and assume a pseudo force equal to a in a direction opposite to its original acceleration, the calculation becomes easier.