Question

Figure shows a uniform iron bar B of weight $30N$ and length $1.40m$. The bar is being used to lift one edge of a concrete slab S. A stone, placed $0.20m$ from one end of B, acts as a pivot. A force of $40N$ pushing down at the other end of B is just enough to lift the slab and hold it as shown.

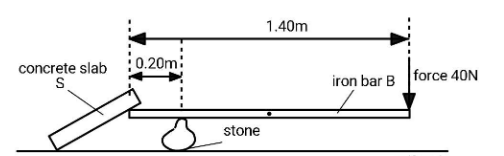
(1) Draw an arrow to show the weight of bar B acting from its centre of mass.
(2) State the distance $d$ of the centre of mass of bar B from the pivot.
(3) Calculate the net clockwise torque acting on the bar B about the pivot.

Answer 1

In order to solve this question, you need to consider the laws of motion and also the concept of torque about a point, in this case, the pivot, which is the point of contact of stone. A normal reaction will act at the point of contact of the concrete slab and also at the pivot. For finding clockwise torque about pivot, you need to consider only two forces, the force of $40N$ that is being applied on the right end and the force of gravitation.

Complete step by step answer:
(1) Let us solve the sub-question first. It is given to you that the iron bar is uniform and therefore the centre of mass of the bar will be located at the centre of the iron bar. Eventually, the weight of the bar will point vertically downward and that too from the centre of the bar as shown:

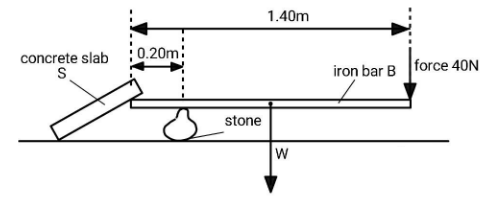
(2) The distance $d$ of the centre of mass of bar B from the pivot will be$d = \dfrac{l}{2} - 0.2$, where $l$ is the length of the iron bar. $d = \dfrac{{1.4}}{2} - 0.2 = 0.5m$

(3) The torque about any point is defined as $\tau = \overrightarrow r \times \overrightarrow F = rF\sin \theta$.From the figure, you can see that the angle between the force and position vector is $90^\circ$.
Therefore, clockwise torque about pivot will be
${\tau _P} = \left( W \right)\left( d \right) + \left( {40} \right)\left( {d + \dfrac{l}{2}} \right) \\\ \Rightarrow{\tau _P} = \left( {30} \right)\left( {0.5} \right) + \left( {40} \right)\left( {0.5 + 0.7} \right) \\\ \therefore{\tau _P} = 63Nm \\\$
Therefore, the weight acts from the centre of the bar, the distance $d = 0.5m$ and the clockwise torque is equal to $63Nm$.

Note: Whenever it is given to you that a rod is uniform, the centre of mass will always be at the centre of the rod and eventually the weight will act from the centre of the rod. Remember that the torque is defined as the cross product of the position vector of the point of contact of the force with the applied force.