Question
Question: Figure shows a two branched parallel circuit with $R_A = 10 \Omega$, $L = \frac{\sqrt{3}}{10} H$, $R...
Figure shows a two branched parallel circuit with RA=10Ω, L=103H, RB=20Ω and C=23mH. Current in L−RA is I1 and in C−RB is I2 and main current is I
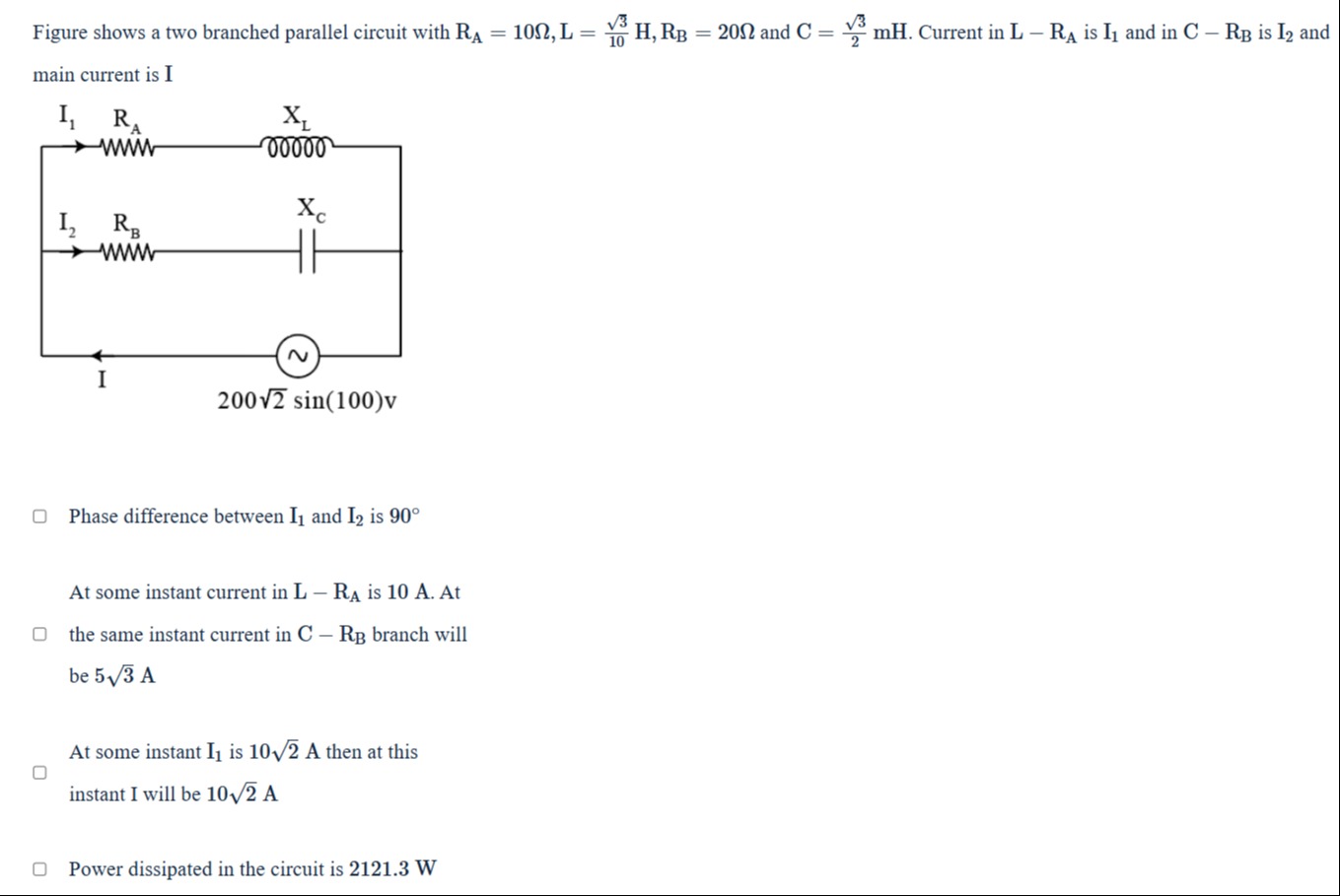
Phase difference between I1 and I2 is 90∘
At some instant current in L−RA is 10 A. At the same instant current in C−RB branch will be 53 A
At some instant I1 is 102 A then at this instant I will be 102 A
Power dissipated in the circuit is 2121.3 W
Phase difference between I1 and I2 is 90∘, At some instant current in L−RA is 10 A. At the same instant current in C−RB branch will be 53 A, At some instant I1 is 102 A then at this instant I will be 102 A
Solution
The circuit consists of two parallel branches connected to an AC voltage source v(t)=2002sin(100t)V. The RMS voltage is Vrms=22002=200V and the angular frequency is ω=100 rad/s.
Branch 1: RA=10Ω, L=103H.
Inductive reactance XL=ωL=100×103=103Ω.
Impedance Z1=RA2+XL2=102+(103)2=100+300=20Ω.
RMS current I1,rms=Z1Vrms=20200=10A.
Phase angle ϕ1=arctan(RAXL)=arctan(10103)=arctan(3)=60∘. Since it is an R-L circuit, the current lags the voltage.
Instantaneous current i1(t)=I1,0sin(ωt−ϕ1)=102sin(100t−60∘)A.
Branch 2: RB=20Ω, C=23mH=23×10−3F.
Capacitive reactance XC=ωC1=100×23×10−31=10032×103=320=3203Ω.
Impedance Z2=RB2+XC2=202+(3203)2=400+9400×3=400+3400=31600=340=3403Ω.
RMS current I2,rms=Z2Vrms=3403200=403200×3=35×3=53A.
Phase angle ϕ2=arctan(RBXC)=arctan(20203/3)=arctan(33)=arctan(31)=30∘. Since it is an R-C circuit, the current leads the voltage.
Instantaneous current i2(t)=I2,0sin(ωt+ϕ2)=53×2sin(100t+30∘)=56sin(100t+30∘)A.
Statement 1: Phase difference between I1 and I2 is 90∘.
The phase of I1 is −60∘ and the phase of I2 is +30∘ relative to the voltage.
The phase difference is ∣30∘−(−60∘)∣=90∘. Statement 1 is correct.
Statement 2: At some instant current in L−RA is 10 A. At the same instant current in C−RB branch will be 53 A.
We need to check if there exists an instant t such that i1(t)=10A and i2(t)=53A.
10=102sin(100t−60∘)⟹sin(100t−60∘)=21.
100t−60∘=45∘ or 135∘ (within one period).
If 100t−60∘=45∘, then 100t=105∘.
i2(t)=56sin(100t+30∘)=56sin(105∘+30∘)=56sin(135∘)=56×21=53A.
Since we found an instant where this is true, statement 2 is correct.
Statement 3: At some instant I1 is 102 A then at this instant I will be 102 A.
I1 refers to the instantaneous current i1(t). The maximum value of i1(t) is 102A. This occurs when sin(100t−60∘)=1.
So, 100t−60∘=90∘+360∘n, which means 100t=150∘+360∘n.
At this instant, 100t+30∘=150∘+30∘+360∘n=180∘+360∘n.
i2(t)=56sin(100t+30∘)=56sin(180∘+360∘n)=56×0=0.
The instantaneous main current i(t)=i1(t)+i2(t).
At the instant when i1(t)=102A, i2(t)=0.
So, i(t)=102+0=102A. Statement 3 is correct.
Statement 4: Power dissipated in the circuit is 2121.3 W.
The average power dissipated in the circuit is the sum of the average power dissipated in each resistor.
Power dissipated in RA: P1=I1,rms2RA=(10)2×10=100×10=1000W.
Power dissipated in RB: P2=I2,rms2RB=(53)2×20=(25×3)×20=75×20=1500W.
Total power dissipated P=P1+P2=1000+1500=2500W.
Statement 4 is incorrect.
All statements 1, 2, and 3 are correct. Since this is a multiple choice question and the provided options are checkboxes, it is implied that there can be multiple correct options.
