Question
Question: Figure shows a torch producing a straight light beam falling on a plane mirror at an angle \({60^0}\...
Figure shows a torch producing a straight light beam falling on a plane mirror at an angle 600. The reflected beam makes a spot P on the screen along the y-axis. If at t=0 the mirror starts rotating about the hinge A with an angular velocity ω=10/sec clockwise, find the speed of the spot P on screen after t=15sec.
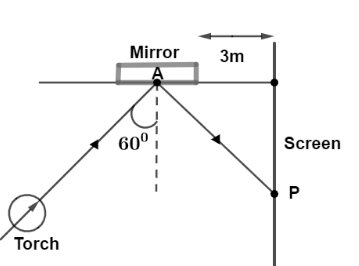
A. 15πmsec−1
B. 30πmsec−1
C. 152πmsec−1
D. 60πmsec−1
Solution
In order to find the speed of spot P, we will find the relation between the distance of spot on y-axis at time t=15sec and when mirror rotates with angular velocity of ω=10/sec then, the reflected ray from mirror will have the twice angular velocity and in time t=15sec mirror will rotate by 150 then the reflected ray will rotate by 300 with the normal.
Complete step by step answer:
Let us first draw the diagram when after t=15sec the reflected and incident ray will make an angle of 300 so, from the geometry of figure we have, <PAB=θ=600 , let BP be the distance on y axis of spot denoted by y.
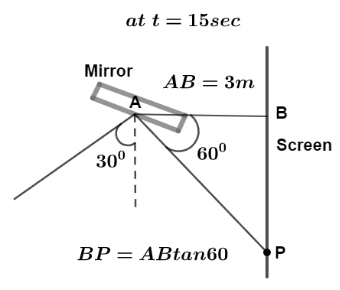
In the right angle triangle ΔABP we have,
tanθ=APBP
⇒y=3tanθ
Differentiate above equation with respect to time, we get
dtdy=3sec2θ.dtdθ dθd(tanθ)=sec2θ
So we get, dtdy=3sec2θ.dtdθ
Now as we know, dtdy is nothing but the velocity of spot P lets denoted as vp. And since the angular velocity of mirror is ω=10persecond the angular velocity of reflected ray will be 2ω=20/sec and dtdθ is nothing but this angular velocity which is 2ω=20/sec
Converting 2ω=20/sec into radian angle we have,
20/sec=1802×π
And, from the diagram we have, this θ=600
Put all the parameters value in equation dtdy=3sec2θdtdθ we get,
vp=3sec2600(1802×π)
⇒vp=3×4×(90π)............sec600=2
∴vp=152πmsec−1
Hence, the correct option is C.
Note: It must be remembered that, the angular speed at which mirror rotates, the reflected ray will rotate by twice the angle with which mirror rotate and hence twice the angular velocity of rotation of reflected ray, and angular velocity of the body is the differentiation of angular displacement with respect to time ω=dtdθ.
