Question

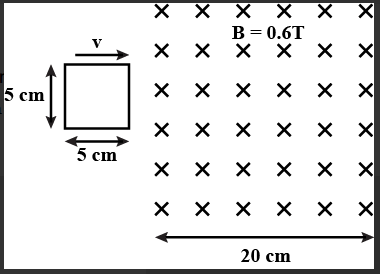
Figure shows a square loop of side $5\;cm\;$ being moved towards right at a constant speed of $1cmse{c^{ - 1}}$ . The front edge just enters the $20\;cm\;$ wide magnetic field at $t = 0$ . Find the induced emf in the loop at $t = 2s\;$ and $t = 10s$ .

\left( A \right)3 \times {10^{ - 2}},zero \\\ \left( B \right)3 \times {10^{ - 2}},3 \times {10^{ - 4}} \\\ \left( C \right)3 \times {10^{ - 4}},3 \times {10^{ - 4}} \\\ \left( D \right)3 \times {10^{ - 4}},zero \\\

Answer 1

Hint : In order to solve this question, we are going to first find the distance travelled by the coil inside the magnetic field in the time interval $t = 2s$ , then, the change in flux can be calculated which gives us the induced emf for this interval, now for $t = 10s$ , coil is completely inside the field, so emf value is accordingly.
The formula for distance covered by the coil moving with velocity $v$ in time $t$
$d = vt$
Flux for magnetic field $B$ through area $A$ is
$\phi = BA$

Complete Step By Step Answer:
As it is given in the question, that the initial speed of the loop is
$u = 1cm{s^{ - 1}}$
Magnetic field, $B = 0.6T$
At $t = 2s$ ,
Distance moved by the coil is
d = vt \\\ \Rightarrow d = 2cm = 2 \times {10^{ - 2}}m \\\
Now, the area under the magnetic field at $t = 2s$
A = 2 \times 5 \times {10^{ - 4}}{m^2} \\\ \Rightarrow A = {10^{ - 3}}{m^2} \\\
Now the initial flux inside the loop is zero because the loop is outside the magnetic field
And the final flux can be calculated as
$\phi = BA = 0.6 \times {10^{ - 3}}$
Therefore, the change in flux becomes
$\Delta \phi = 0.6 \times {10^{ - 3}}$
Therefore, the induced emf for the square loop is
e = \dfrac{{\Delta \phi }}{{\Delta t}} = \dfrac{{0.6 \times {{10}^{ - 3}}}}{2} = 0.3 \times {10^{ - 3}}V \\\ \Rightarrow e = 3 \times {10^{ - 4}}V \\\
We are given the velocity is $1cmse{c^{ - 1}}$ , and the distance inside the field that the loop is travelling is $20cm$ , therefore, the time period is $20\sec$
Therefore, at time $t = 10s$ , the coil is completely inside the magnetic field, hence there is no change in the magnetic flux at that time, so the induced emf is equal to zero.
Hence, option $\left( D \right)3 \times {10^{ - 4}},zero$ is correct.

Note :
The induced emf depends upon the change in the flux in the loop which can be caused due to any of the reasons like entering or leaving a magnetic field, change in the value of magnetic field due to change in current, but when a coil moves just inside the field with no change in the field, the flux is zero.