Question
Question: Figure shows a square current loop ABCD of side 2 m and current \[I = \dfrac{1}{2}\,{\text{A}}\]. Th...
Figure shows a square current loop ABCD of side 2 m and current I=21A. The magnetic moment M of the loop is:
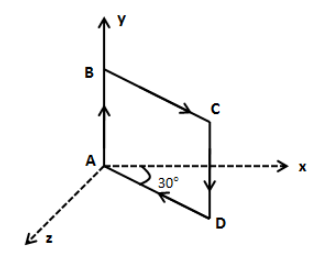
A. (i^−3k^)A−m2
B. (j^−k^)A−m2
C. (3i^−k^)A−m2
D. (i^−k^)A−m2
Solution
Calculate the magnitude of the magnetic moment. The direction of magnetic moment is along the direction of the area vector. Express the magnetic moment in terms of its two components and substitute the values of angle made by the area vector with the x-axis.
Formula used:
The expression for magnetic moment of the current carrying loop,
M=NIA
Here, N is the number of turns of the loop, I is the current flowing through the loop and A is the cross-sectional area of the current loop.
Complete step by step answer:
We have the expression for magnetic moment of the current carrying loop,
M=NIA
Here, N is the number of turns of the loop, I is the current flowing through the loop and A is the cross-sectional area of the current loop.
Let’s calculate the magnitude of the magnetic moment of the loop as follows,
M=NIA
Since N is equal to 1. We have,
M=IA
⇒M=I(AB×BC)
Substituting I=21A for I, 2 m for AB and 2 m for BC in the above equation, we get,
M=(21)(2×2)
⇒M=2A−m2
We know that the direction of magnetic moment is along the direction of the area vector. The direction of the area vector in the above loop is perpendicular to the plane of the loop as shown in the figure.
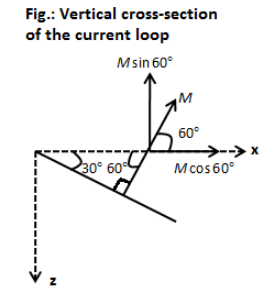
In the above figure, M is the direction of the magnetic moment which is the direction of the area vector of the loop. Now, we can express the magnetic moment of the above current loop as follows,
M=Mcos60∘i^−Msin60∘k^
Substitute 2A−m2 for M in the above equation, we get,
M=(2)(21)i^−(2)(23)k^
∴M=(i^−3k^)A−m2
So, the correct answer is option (A).
Note: To solve these types of questions, always first determine the magnitude of the magnetic moment and then express it in the vector form. In this solution, the angle between the current loop and x-axis is 30∘ but the angle made by the magnetic moment vector with the x-axis is 60∘. Z-component of the magnetic moment is along the negative z-axis therefore it is taken as negative.
