Question
Question: Figure shows a square current-carrying loop ABCD of side \[10\;{\rm{cm}}\] and current \[i = 10\;{\r...
Figure shows a square current-carrying loop ABCD of side 10cm and current i=10A. The magnetic moment M of the loop is:
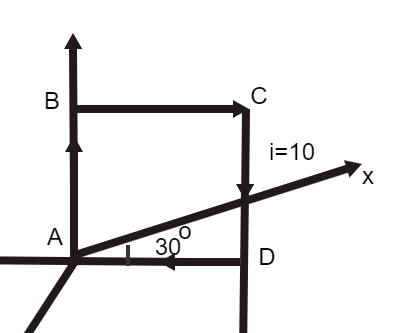
Solution
The above problem can be resolved using the concepts and fundamentals of the magnetic moment, along with the fundamentals of the vector cross product. The magnetic moment is nothing but can be considered as the significant property of any magnetised material which when coming in contact of the magnitude of the external magnetic field, tends to develop a mechanical moment at any point.
Complete step by step answer:
The angle between AD and AX is, θ=30∘.
The length of side is, d=10cm=10cm×100cm1m=0.1m.
The magnitude of current is, i=10A.
The expression for the moment of the loop is,
M=i(AD×AB)…………………………………….(1)
The vector AD is given as,
