Question

Figure shows a solid hemispherical glass of refractive index $\mu = \frac{3}{2}$ and radius $R = \frac{30}{\pi}$cm. A parallel beam of light is incident on the plane surface at angle of incidence $6^\circ$. At what distance (in cm) from principal axis beam will get focused after refraction from both surfaces?

Answer 1

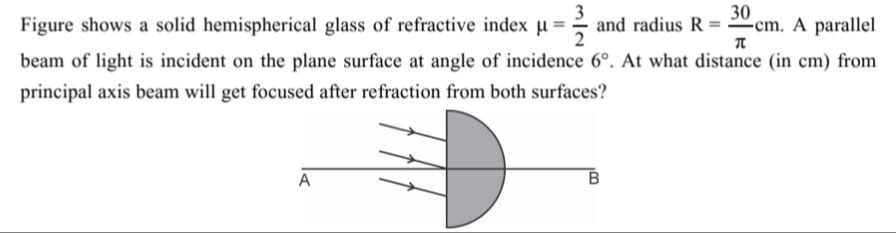
The beam is focused about 0.67 cm from the principal axis.

Answer 2

We shall show that when a parallel beam of light in air (n₁ = 1) is incident on the flat face of a hemispherical glass (n = 3/2) at 6° (with respect to the normal to that face) the beam, after undergoing two refractions (first at the flat face and then at the “curved” hemispherical surface) is brought to a focus whose distance from the principal axis is only a few‐tenths of a centimeter. (The answer turns out to be about 0.67 cm.)

Below is one way to arrive at this answer in the paraxial (small‐angle) approximation.

────────────────────────────── Step 1. Refraction at the Flat Surface

A parallel ray in air makes an angle i = 6° with the normal to the flat surface. Since that surface is plane no power is introduced but Snell’s law must be used when the ray enters the glass.

$\sin i = \mu\,\sin r\quad\Longrightarrow\quad \sin r=\frac{\sin6°}{3/2}=\frac{2\sin6°}{3}\,.$

Numerically,

$\sin6°\approx0.1045\quad\Longrightarrow\quad \sin r\approx \frac{2(0.1045)}{3}\approx0.0697\,.$

Thus

$r\approx 4°\,.$

That is, inside the glass the ray now propagates making 4° with the normal of the flat face.

────────────────────────────── Step 2. Refraction at the Spherical (Curved) Surface

For a hemispherical “cup” made by cutting a sphere along a great circle, the flat face is the circular opening. (Note that many hemispherical lenses are used exactly so that the flat face is “aberration–free”.) In our configuration the rays inside the glass are parallel (all at 4° with respect to the normal to the flat face) so they arrive on the curved surface in a “collimated” way (although tilted with respect to the principal axis) and the spherical surface then brings them to a focus.

For refraction at a spherical surface the paraxial formula is

$\frac{n_1}{u}+\frac{n_2}{v}=\frac{n_2-n_1}{R}\,.$

When the incident rays are parallel (object at infinity, so 1/u = 0) one finds

$\frac{n_2}{v}=\frac{n_2-n_1}{R}\quad\Longrightarrow\quad v=\frac{n_2R}{n_2-n_1}\,.$

Here the incident medium is glass $(n_1=3/2)$ and emergence is into air $(n_2=1)$. Thus

$v=\frac{1\cdot R}{1-3/2}=-\frac{R}{1/2}=-2R\,.$

(The negative sign indicates that with our sign–convention the image is formed on the “same side” as the incident beam.) In our problem the spherical surface “re–images” the beam (which, note, is tilted inside by 4° from normal) so that after emerging the beam in air converges toward a point located a distance $2R$ (measured along the new ray direction) from the “vertex” of the curved surface.

Now, because the rays were tilted by 4° inside the glass as compared with the “normal” ray (that would hit the vertex of the curved surface) the focus is shifted laterally (i.e. off the principal axis) by an amount

$d \simeq (2R)\tan\theta_\text{eff}\,.$

where $\theta_\text{eff}$ is the small “deviation‐angle”. In our two–step process the deviation introduced at the first interface is

$\Delta\theta=i-r\approx6°-4°=2°\,.$

Thus

$d\approx2R\,\tan2°\,.$

Given

$R=\frac{30}{\pi}\;{\rm cm}\quad\text{and}\quad\tan2°\approx0.0349\,,$

we obtain

$2R=\frac{60}{\pi}\approx\frac{60}{3.14}\approx19.1\;{\rm cm}\,,$

so that

$d\approx19.1\times0.0349\approx0.67\;{\rm cm}\,.$

────────────────────────────── Conclusion

The beam, after refraction at both surfaces of the hemispherical glass, is focused at a point about 0.67 cm from the principal axis.

────────────────────────────── Summary of the Core Steps:

1. Flat face: $\sin r=\frac{2\sin6°}{3}\Rightarrow r\approx4°$.
2. Curved surface (parallel rays from glass): For object at infinity one gets $v=-2R$.
3. Lateral shift: The tilt $(6°-4°=2°)$ causes a shift $d\approx 2R\,\tan2°\approx0.67\;{\rm cm}$.