Question
Question: Figure shows a small time elapsed before the block separated from the plank. Block A of mass \(m\) k...
Figure shows a small time elapsed before the block separated from the plank. Block A of mass m kept at the left end of a plank B of mass M=2m and length l. The system can slide on a horizontal road. The system is started towards right with the initial velocity v. The friction coefficient between the road and plank is 21 and that between the plank and the block is 41. Find the time elapsed before the block separates from the plank.
Solution
To find the time taken for the block A to fall from plank B we can use the equations of motion. Here the distance the block needs to cover in before falling is l and the block initially starts from rest, thus we need to find the acceleration of the block A with respect to B
Formula used:
f=μmg
s=ut+21at2
Complete step by step answer:
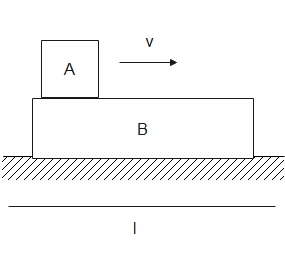
Consider the step-up as given in the figure above. Let the mass of the block A be m and that of B be M. Given that M=2m , also the length of the B plank is l long, is placed on a road. Let it move with a velocity v, as shown below.
Clearly, when this system is moved, there exists friction. Since friction is a contact force, here there are two frictions, which act on the system. They are at the road - plank interface and the plank-block interface.
Also, given that coefficient of friction between the road and plank is 21 and that between the plank and the block is 41.
Now consider the system is displaced, such that after time t, the block A will fall from the plank. Let us look at the individual blocks, then we have, fa and fb to be the friction acting on the A and B respectively.
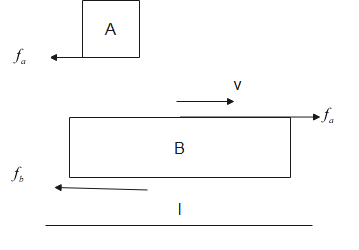
Clearly, fa=μmg=4mg and fb=μ(M+m)g=23mg
Then the retardation due to friction is given as
aa=mfa=4mmg=4g
ab=Mfb−fa=2m(23mg−4mg)=85g
From the above equations, clearly, ab>aa. This implies that the after t the block will fall down from the plank B.
Then the relative density of block A with respect to the plank B is given as
a=ab−aa=85g−4g=83g
Then, here, u=0 and a=83g and s=l, from the equation of motion, s=ut+21at2, we can say that
l=21×83g×t2
⟹t=43l
Thus the time elapsed before the block separates from the plank is 43l.
Note: Here there are two surfaces and hence, the system has two contact forces. Since both the friction act on the plank B in the opposite direction, to find the net retardation we need to subtract both the friction. And then use the acceleration to find the time taken for the block to separate from the plank.
