Question

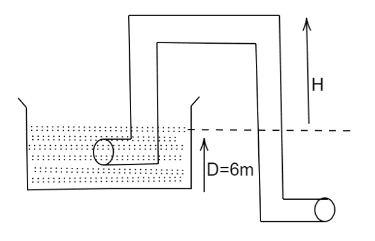
Figure shows a siphon, the vessel area is very large as compared to the cross-section of the tube. Tube has a uniform cross section, its lower end is $6m$ below the surface of water. What is the maximum height $H$ (in $m$ ) of the upper end for siphon to work? Take density of water $= {10^3}\dfrac{{kg}}{{{m^3}}}$ , atmospheric pressure $= {10^5}\dfrac{N}{{{m^2}}}$ .

Answer 1

Use Bernoulli’s theorem which gives the relation between density, pressure, and height of the fluid above the object. In the above situation, atmospheric pressure will be equal to the pressure exerted by a liquid, using this and putting values in Bernoulli’s equation we will find the required maximum height.
$P = \rho gh$
Where $P$ is the pressure, $\rho$ is the density of water, $g$ is the gravitational force, and $h$ is the height of fluid above the object.

Complete step by step answer:
When a fluid is contained within a container, the depth of an object submerged in the fluid can be determined. The greater pressure an object experiences the deeper it is submerged in the fluid. Because of the weight of the fluid above it, this is the case. Due to the weight of the fluid, the more pressure is put on the submerged object the denser the fluid above it is.
Given the density of water $= {10^3}\dfrac{{kg}}{{{m^3}}}$
${P_{atm}} = {10^5}\dfrac{N}{{{m^2}}}$
According to the question, at the highest point of siphon let it be $P$ the atmospheric pressure will be equal to pressure due to liquid being up to height in siphon. Total height is $H + 6$
Therefore, ${P_{atm}} = \rho g(H + 6)$
$\Rightarrow {10^5} = {10^3} \times 10(H + 6)$
$\Rightarrow 10 = H + 6$
$\Rightarrow H = 4m$
Hence, the maximum height $H$ (in $m$ ) of the upper end for the siphon to work is $4m$ .

Note:
The pressure at a specific place in a pipe is affected by the changes in fluid elevation that occur as fluid travels through a piping system where pipes rise and fall, changing height. As a result, as the fluid rises, the pressure in the pipe decreases and as the fluid level drops, the pressure in the pipe rises.