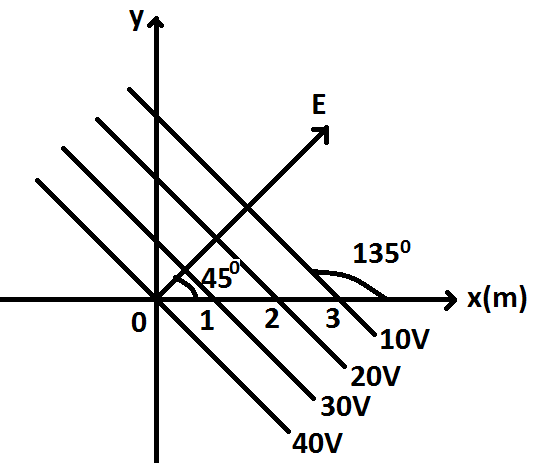
Question

Figure shows a set of equipotential surfaces. The magnitude and direction of electric field that exists in the region is:

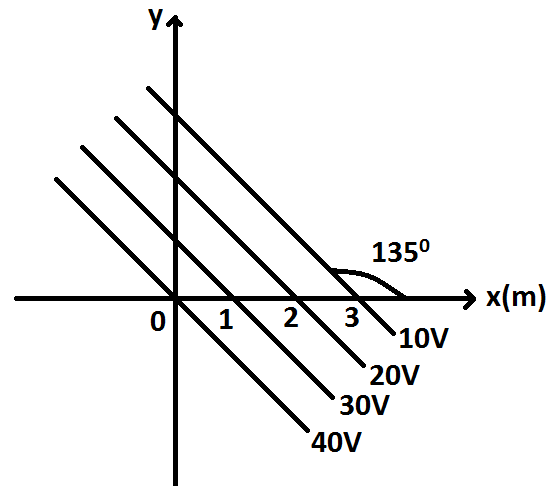
(A) $10\sqrt 2 V/m$ at ${45^ \circ }$ with x-axis
(B) $10\sqrt 2 V/m$ at $- {45^ \circ }$ with x-axis
(C) $5\sqrt 2 V/m$ at ${45^ \circ }$ with x-axis
(D) $5\sqrt 2 V/m$ at $- {45^ \circ }$ with x-axis

Answer 1

Hint : We know that the electric field of the region is perpendicular to the equipotential surfaces. Therefore, we will find the horizontal and vertical component of the electric field. After that, using these both components, we will find the angle with the horizontal.

Complete Step By Step Answer:
By applying the rules of geometry, we can determine the angles and dimensions on the y-axis as shown in the figure.

Now, we will find the horizontal component of the electric field.
${E_x} = \dfrac{{ - dV}}{{dx}} = \dfrac{{ - \left( {30 - 40} \right)}}{{2 - 1}} = 10i$
Similarly, the horizontal component of the electric field can be determined.
${E_y} = \dfrac{{ - dV}}{{dy}} = \dfrac{{ - \left( {30 - 40} \right)}}{{2 - 1}} = 10j$
We know that the electric field is given by the addition of its horizontal and vertical component.
$E = {E_x} + {E_y} = 10i + 10j$
The magnitude of this electric field is given by:
$\sqrt {{{10}^2} + {{10}^2}} = 10\sqrt 2 V/m$ .
Now to find the tangent of the angle made by the electric field with the horizontal, we need to divide its vertical component by its horizontal components.
Let us consider that the electric field is making angle $\theta$ with the x-axis.
$\Rightarrow \tan \theta = \dfrac{{dy}}{{dx}} = \dfrac{1}{1} = 1 \\\ \Rightarrow \theta = {45^ \circ } \\\$
Hence, option A is the right answer.

Note :
Here, we have determined the magnitude and the direction of the electric field. We also know that it is perpendicular to the equipotential surfaces. Thus, if we want to indicate the electric field in the diagram, we can show it accordingly as shown in the following figure.