Question

Figure shows a rod of length 20 cm pivoted near an end and which is made to rotate in a horizontal plane with a constant angular speed. A ball of mass m is suspended by a string also of length 20 cm from the other end of the rod. If the angle $\theta$ made by this string with the vertical is 30, the angular speed of the rotation will be?
Take $g = 10$ $m/{s^2}$.

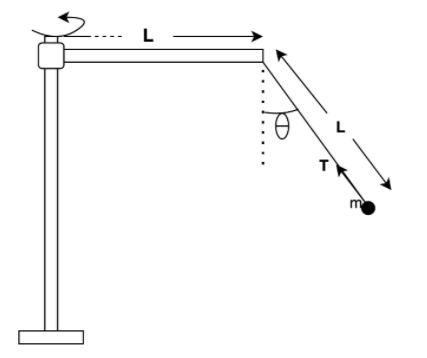
A. $\omega = 8$ radians/sec.
B. $\omega = 4.4$ radian/sec.
C. $\omega = 14.4$ radian/sec.
D. $\omega = 4.4$ radian/sec.

Answer 1

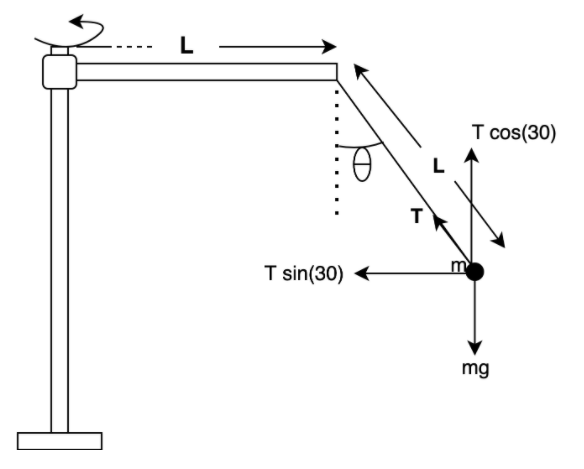
Angular velocity refers to how fast an object changing its angular orientation with time. From the following diagram, it is clear that the ball is moving in a circular path. When a body moves in a circular path then the centripetal force is always there which acts towards the center of the circular path. The centripetal force, in this case, is balanced by the $T\sin (30)$. Where $T$ is the tension in the string due to mass $m$ . Now it is making sense that we can obtain an equation of centripetal force and the $\sin$ component of the tension in the string. On the other hand, we can see that to rotate in the fixed circular path $T\cos (30)$ must be balanced with the force $mg$ . By solving the above two equations we will reach the desired result.

Complete step by step answer:

Step 1:
Express the formula for the centripetal force in terms of angular speed.
$\therefore F = m{\omega ^2}r$.
Where $m$ is mass, $\omega$ its angular velocity and $r$ is the radius of the path.
Step 2: If the length of the string is $L$ then the radius of the path will be $L + L\sin \theta$ because the angle made by the string with vertical is $\theta = 30$ . Now we will put the $L + L\sin \theta$ for $r$ . We know that the centripetal force is balanced with the sine component of the tension in the string, therefore we can write the following equation.
$\therefore T\sin (30) = m{\omega ^2}(L + L\sin (30))$. -----(1).
Step 3: The force acting upward $T\cos (30)$ is balanced with the force $mg$ .
$\therefore T\cos (30) = mg$ . ------(2).
Step 4: Now divide equation (1) by equation (2).
$\therefore \dfrac{{T\sin (30)}}{{T\cos (30)}} = \dfrac{{m{\omega ^2}(L + L\sin (30))}}{{mg}}$
$\Rightarrow \tan (30) = \dfrac{{{\omega ^2}(L + L\sin (30))}}{g}$
Step 5: Take ${\omega ^2}$ one side and all the remaining terms on the other side.
$\therefore {\omega ^2} = \dfrac{{\tan (30) \times g}}{{L + L\sin (30)}}$
Step 6: Substitute the value 0.2 m for the $L$ and 10 $m/{s^2}$ for $g$
$\therefore {\omega ^2} = \dfrac{{10 \times \dfrac{1}{{\sqrt 3 }}}}{{0.2 + 0.2 \times \dfrac{1}{2}}}$
$\Rightarrow \omega = \sqrt {\dfrac{{10 \times \dfrac{1}{{\sqrt 3 }}}}{{0.3}}}$
$\Rightarrow \omega = 4.4$ radian/sec.

Hence, the correct answer is option (D).

Note: Sometimes angular velocity and angular speed may be confusing. The difference between angular velocity and angular speed is the same as the difference between speed and velocity. Angular speed tells us how fast a body is moving with respect to time, while angular speed tells us how fast a body is moving in a particular direction (clockwise or anti-clockwise).