Question

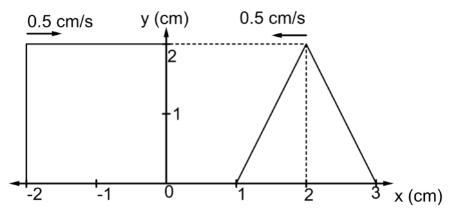
Figure shows a rectangular pulse and a triangular pulse approaching each other along the x – axis. The pulse speed is $0.5{\text{ }}cm/s$. What is the resultant displacement of medium particle due to superposition of wave at $x{\text{ }} = {\text{ }}0.5{\text{ }}cm$ and $t{\text{ }} = {\text{ }}2{\text{ }}s$.

A. $3.5{\text{ }}cm\:$
B. $2.5{\text{ }}cm\:$
C. $4{\text{ }}cm\:$
D. $3{\text{ }}cm\:$

Answer 1

We will use the concept of speed and distance travelled. Then, we will also use the concept of similarity of triangles for finding the maximum displacement of the waves. Finally, we will add up the individual maximum displacement and evaluate the resultant displacement and then select the suitable option.

Complete step by step answer:
We are given that the triangular wave moves towards the left with speed of $0.5{\text{ }}cm/s$ and we are asked to find the answer after $2{\text{ }}s$. Thus, the triangular wave moves a distance of
${x_1}{\text{ }} = {\text{ }}vt{\text{ }} = {\text{ }}0.5{\text{ }} \times {\text{ }}2{\text{ }} = {\text{ }}1{\text{ }}cm$ towards left.
Hence, the midline of the triangular will lie on the mark of $1$ on the x – axis.

Now, the displacement in the y – axis will be
${y_1}{\text{ }} = {\text{ }}2{\text{ }}cm$
Now, similarly the rectangular wave will also move $1{\text{ }}cm$ towards the right.
Thus, the extreme left line of the rectangular wave will coincide with the mark of $- 1{\text{ }}cm$ on the x – axis.Now, we will draw a line from the $0.5{\text{ }}cm$ mark on the x – axis parallel to the midline of the triangular pulse. The length of this line will signify the maximum displacement of the rectangular pulse.

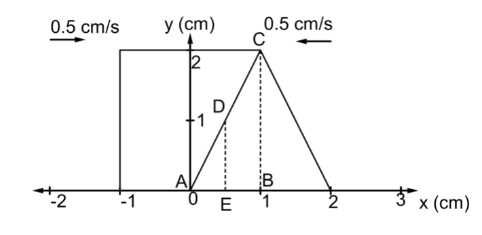
Now, we will use the concept of similarity of triangles. Here, in the diagram clearly,
$\Delta ABC{\text{ }} \sim {\text{ }}\Delta AED$
Thus, by idea of corresponding parts of similar triangles, we can write
$\dfrac{{BC}}{{ED}}{\text{ }} = {\text{ }}\dfrac{{AB}}{{AE}}$

Now, $ED$ is the maximum displacement of the rectangular pulse.Now, the values of the other parameters are
$BC{\text{ }} = {\text{ }}2{\text{ }}cm$
$\Rightarrow AB{\text{ }} = {\text{ }}1{\text{ }}cm$
$\Rightarrow AE{\text{ }} = {\text{ }}0.5{\text{ }}cm$
Putting in these values, we get
$\dfrac{2}{{ED}}{\text{ }} = {\text{ }}\dfrac{1}{{0.5}}$
Further, we get
$ED{\text{ }} = {\text{ }}1{\text{ }}cm$
Thus,
${y_2}{\text{ }} = {\text{ }}1{\text{ }}cm$
Hence, the resultant displacement is
$y{\text{ }} = {\text{ }}{y_1}{\text{ }} + {\text{ }}{y_2}$
Substituting the values, we get
$\therefore y{\text{ }} = {\text{ }}2{\text{ }} + {\text{ }}1{\text{ }} = {\text{ }}3{\text{ }}cm$

Hence, the correct answer is D.

Note: Students should be careful while selecting the triangles for similarity comparison as selecting the wrong triangles will lead them to wrong answers. Students should be very much careful while substituting the values.