Question

Figure shows a process on a gas in which both pressure and volume change. The molar heat capacity for this process is C

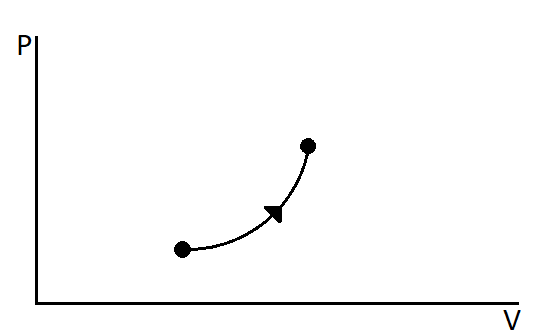
(A) $C = 0$
(B) $C = {C_V}$
(C) $C > {C_V}$
(D) $C < {C_V}$

Answer 1

We need to draw another path from the initial and the final point, which will consist of 2 lines. Then we need to find the sum of the work done and the internal energy for both these paths which is the heat supplied. By dividing that with temperature, we will get the specific heats and their relation.
Formula used: In this solution we will be using the following formula,
$\Rightarrow dQ = dU + dW$
where $Q$is the heat, $U$ is the internal energy and $W$ is the work done.

Complete step by step answer:
To solve this let us redraw the diagram with another path between the initial and final points which is parallel to pressure and the volume axis.

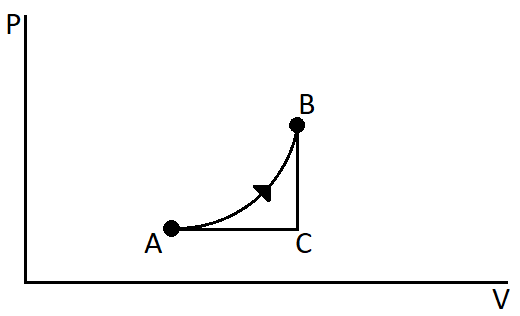
So in between the points A and B we have drawn another path ACB. The line AC is parallel to the volume axis and the path CB is parallel to the pressure axis.
Let us consider $C$ as the molar heat capacity and ${W_{AB}}$ as the work done for the process AB. The process ACB can be considered as the sum of the 2 processes Ac and CB. Since the process AC is parallel to the volume axis, so the pressure is constant. Hence the molar specific heat capacity of this process will be ${C_P}$. And the process CB is parallel to the pressure axis. So the volume is constant. Hence the molar specific heat capacity for the process CB will be ${C_V}$.
Now since the initial and the final point of both the process AB and ACB are the same, and the internal energy is a state function so it doesn’t depend on the path followed in the process, so the internal energy of both the processes AB and ACB are the same.
The work done for a process is the area under the curve of that process. From the graph we can see that the area under the curve in the process AB is more than the area under the curve of the process ACB.
Hence we can write,
$\Rightarrow {W_{AB}} > {W_{ACB}}$
Now we can add the internal energies on both the sides since it is same for both the processes,
$\Rightarrow {W_{AB}} + {U_{AB}} > {W_{ACB}} + {U_{ACB}}$
Now according to the first law of thermodynamics, $dQ = dU + dW$, the sum of the work done and the internal energy of a system is equal to the heat supplied to the system.
Hence, ${W_{AB}} + {U_{AB}} = {Q_{AB}}$ and ${W_{ACB}} + {U_{ACB}} = {Q_{ACB}}$
So substituting these in the equation we get,
$\Rightarrow {Q_{AB}} > {Q_{ACB}}$
Now the heat supplied for the process ACB can be broken as,
$\Rightarrow {Q_{ACB}} = {Q_{AC}} + {Q_{CB}}$
Therefore, we get
$\Rightarrow {Q_{AB}} > {Q_{AC}} + {Q_{CB}}$
Now we divide both the sides with temperature. This gives us the molar specific heat capacities for all the processes,
$\Rightarrow C > {C_P} + {C_V}$
Hence the molar specific heat capacity C is greater than the sum of ${C_P}$ and ${C_V}$. As ${C_P}$ and ${C_V}$ are positive, so C is greater than only ${C_V}$.
Therefore, $C > {C_V}$.
So the correct answer will be option (C).

Note:
The molar specific heat capacity of a substance is the amount of energy that must be added in the form of heat to one mole of a substance so as to increase its temperature by unit amount. It has a unit of joule per Kelvin per mole, that is, $J{K^{ - 1}}mo{l^{ - 1}}$.