Question

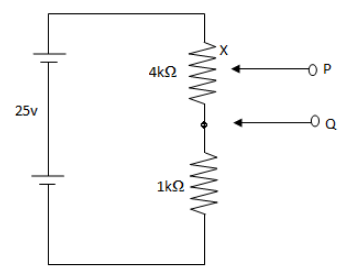
Figure shows a potential divider circuit, which by adjustment of the position of the contact X, can be used to provide a variable potential difference between the terminals P and Q. What are the limits of this potential difference?

A. $0$ and $20\,{\text{mV}}$
B. ${\text{5}}$ and $25\,{\text{mV}}$
C. $0$ and $20\,{\text{V}}$
D. $0$ and $25\,{\text{V}}$

Answer 1

We are asked to find the lower limit and upper limit of potential difference between the terminals P and Q. To find the lower limit move the terminal P to the lower end of resistor ${\text{4}}\,{\text{k}}\Omega$ and to find the upper limit, move the terminal P to the upper end of resistor ${\text{4}}\,{\text{k}}\Omega$.

Complete step by step answer:
We are given a circuit and asked to find the range of potential difference between the terminals P and Q.Let us first find the lower limit of the potential difference between the terminals P and Q.We can find the lower limit of potential difference by moving the terminal P to the lower end of ${\text{4}}\,{\text{k}}\Omega$ resistor that is towards terminal Q. In this case, the potential difference between P and Q will be zero. Therefore, the lower limit of the potential difference between the terminals P and Q will be $0\,{\text{V}}$.

Now, we find the upper limit of potential difference between the terminals P and Q. In this case we move the terminal P to the upper end of ${\text{4}}\,{\text{k}}\Omega$ resistor that is away from the terminal Q.Here, let $i$ be the current flowing through the circuit.
We redraw the circuit.

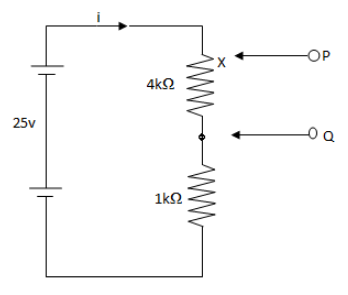
Here, the equivalent resistance will be,
$R = {\text{4}}\,{\text{k}}\Omega + 1\,{\text{k\Omega }}$
$\Rightarrow R = 5\,{\text{k}}\Omega$
Current through a circuit is,
${\text{voltage}} = {\text{current}} \times {\text{resistance}}$ (i)
Here, voltage is $25\,{\text{V}}$
Putting the values of voltage and equivalent resistance in equation (i) we get,
$25\, = i \times 5$
$\Rightarrow i\, = \dfrac{{25}}{5} = 5\,{\text{A}}$
Now, voltage across the resistor ${\text{4}}\,{\text{k}}\Omega$ will be (using equation (i))
${V_{PQ}} = i \times 4$
Putting the value of $i$ in the above equation we get,
${V_{PQ}} = 5 \times 4$
$\therefore {V_{PQ}} = 20\,{\text{V}}$
Therefore, the upper limit of potential difference between the terminals P and Q is $20\,{\text{V}}$.So, the limits of potential difference between the terminals P and Q are $0\,{\text{V}}$and $20\,{\text{V}}$.

Hence, the correct answer is option C.

Note: Using a potential divider circuit, we can get different voltages from a common supply voltage. One example of a potential divider is potentiometer. Potential divider circuits can be used for controlling audio volume, for controlling temperature in the freezer.