Solveeit Logo
Login

Question

Question: Figure shows a part of an electric circuit. The potentials at the points a, b and c are 30V, 12V and...

Figure shows a part of an electric circuit. The potentials at the points a, b and c are 30V, 12V and 2V respectively. Find the currents through the three resistors.

Explanation

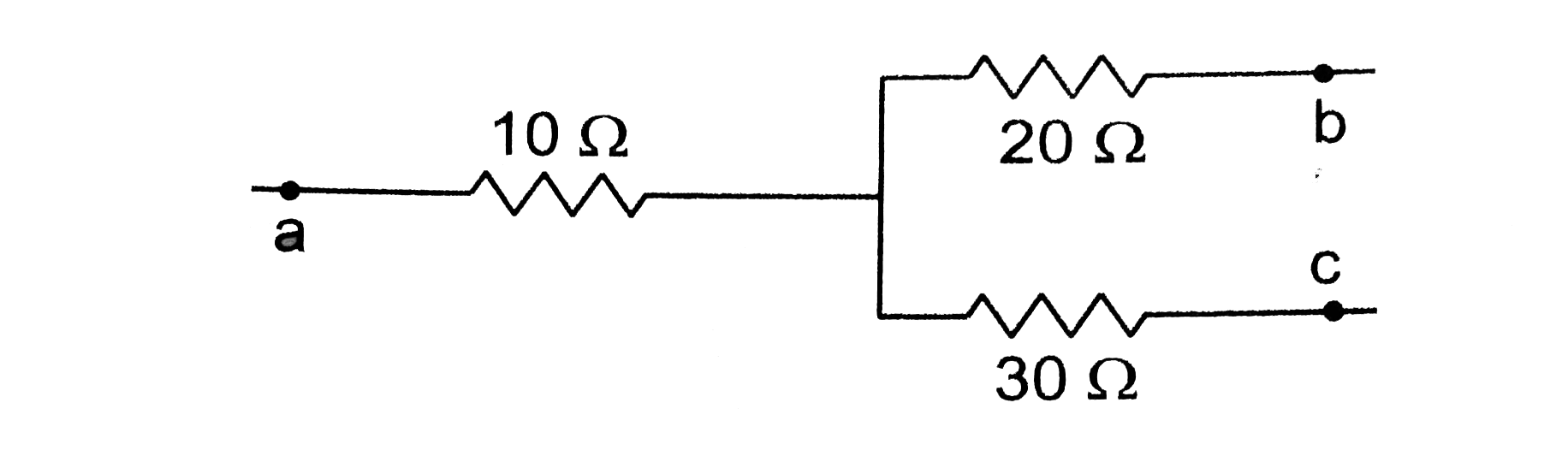
Solution

Hint : To answer this question, we first need to understand what an electric circuit is. A channel for transmitting electric current is known as an electric circuit. An electric circuit consists of a device, such as a battery or a generator, that provides energy to the charged particles that make up the current; equipment that uses current, such as lamps, electric motors, or computers; and the connecting wires or transmission lines.

Complete Step By Step Answer:
KVL- Kirchhoff's circuit rules are two equalities in the lumped element model of electrical circuits that deal with current and potential difference. Gustav Kirchhoff, a German physicist, was the first to describe them in 1845. This broadened Georg Ohm's work and came before James Clerk Maxwell's.
KCL- Kirchhoff's circuit rules are two equalities in the lumped element model of electrical circuits that deal with current and potential difference. Gustav Kirchhoff, a German physicist, was the first to describe them in 1845. This broadened Georg Ohm's work and came before James Clerk Maxwell's.

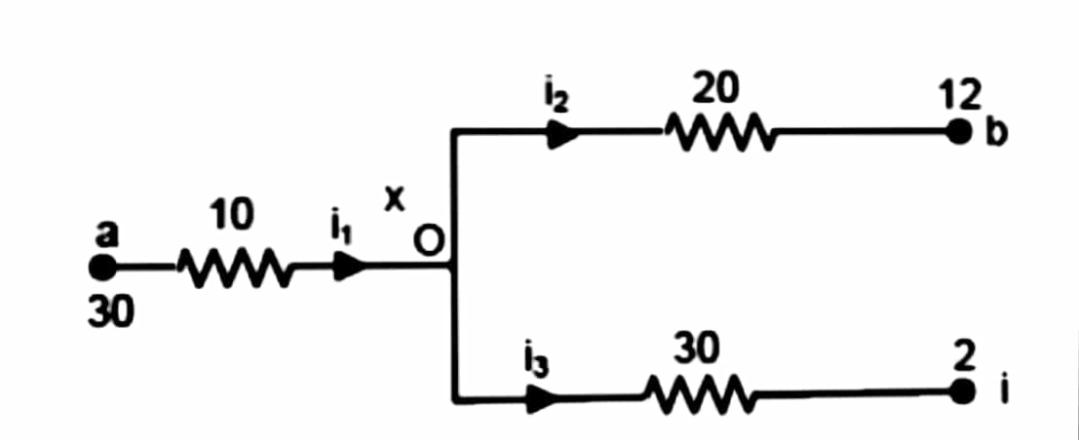
Let us assume that potential at O is V volts.
Applying ohm's law at each branch –
(30−V)=10i1(30 - V) = 10{i_1}
(V−12)=20i2(V - 12) = 20{i_2}
(V−2)=30i3(V - 2) = 30{i_3}
And by KCL we know that at point O
i1=i2+i3{i_1} = {i_2} + {i_3}
Putting values
30−V10=V−1220+V−230\dfrac{{30 - V}}{{10}} = \dfrac{{V - 12}}{{20}} + \dfrac{{V - 2}}{{30}}
30−V=V−122+V−2330 - V = \dfrac{{V - 12}}{2} + \dfrac{{V - 2}}{3}
30−V=3V−36+2V−4630 - V = \dfrac{{3V - 36 + 2V - 4}}{6}
180−6V=5V−40180 - 6V = 5V - 40
11V=22011V = 220
V=20voltsV = 20volts
Putting values in current equations of each branch
So the final values of current are -
i1=30−2010=1A i2=20−1220=0.4A i3=20−230=0.6A{i_1} = \dfrac{{30 - 20}}{{10}} = 1A \\\ {i_2} = \dfrac{{20 - 12}}{{20}} = 0.4A \\\ {i_3} = \dfrac{{20 - 2}}{{30}} = 0.6A

Note :
Circuit analysis of more complex circuits is possible thanks to Kirchhoff's two laws. The technique is simple, despite the fact that the algebraic procedures are still somewhat complicated. These laws are widely used in the field of electrical engineering.