Question
Question: Figure shows a parallel system of four forces and two couples. (i) Replace it by a single force a...
Figure shows a parallel system of four forces and two couples.
(i) Replace it by a single force and obtain its location from point A
(ii) Replace it by a force couple system at point A
(iii) Replace it by a force couple system at point D
(iv) Replace it by two parallel forces at B and D
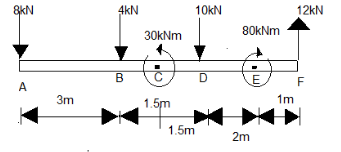
Solution
In order to solve this question, we are going to calculate the torque at point A, then considering a variable for the distance and dividing by force and equating to the torque, distance is calculated. Similarly, other parts are solved for the other values of forces and torques as well.
Formula used: Torque at any point is given by
⇒τA=FA×x
Complete step by step solution:
Let us consider the point A , the torque at the point A is due to the forces 4kN , 10kN and 12kN , also due to the two couple forces 30kNm and 80kNm , thus, if we find the torque about the point A , then,
τA=4kN×3+10kN×6−30kNm+80kNm−12kN×9 ⇒τA=12+60−30+30−108 ⇒τA=152−138 ⇒τA=14kNm
Now as we know that the net torque can be related to the net force as
⇒τA=FA×x
Putting values of net force at A and the net torque at A to find the distance
⇒14kNm=10kN×x ⇒x=1.4m
Now if we find the net force at the point A in y−direction
Fnet=−8−4−10+12 ⇒Fnet=−10kN
The net torque about A is
τnet=4kN×3m+10kN×6m−30kNm+80kNm−12kN ⇒τnet=12+60−30+80−108 ⇒τnet=152−138 ⇒τnet=14kNm
Now at point D ,
The net torque is
τD=8kN×4.5m+4kN×1.5m−30kNm+10kN×1.5m+80kNm−12kN×3m ⇒τD=3.6+6−30+15+80−36 ⇒τD=38.6kNm
At point B and D
The net force is
FB=−8−4−10+12−1.530+580 ⇒FB=−14kN
These two parallel forces are of magnitude 14kN each but in opposite directions.
Note:
The forces to replace the two couple forces are calculated step by step at all the points, when we needed to find the couple forces the torques were calculated while in the other parts, where directly the forces were asked, the force was calculated at that point.
