Question
Question: Figure shows a parabolic mirror with the equation of section on the XY plane as \[{{y}^{2}}=4ax\]. A...
Figure shows a parabolic mirror with the equation of section on the XY plane as y2=4ax. A light ray parallel to X-axis is incident on the mirror at a point M with abscissa 4a. The unit vector along the reflected ray will be
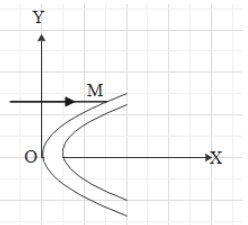
Solution
Here we have to find the unit vector along the reflected ray. We have given abscissa which is the coordinate of X-axis at the point of intersection i.e. point at which light is incident. An equation of parabola for the given case. So by using the parabolic equation we can find the Y-coordinate. Once we find the coordinate and apply the laws of reflection for spherical mirrors and by finding slope we can find the unit vector.
Formula used:
u=a2+b2ai∧+bj∧
Complete answer:
Parabolic mirror can be convex mirror or concave mirror, here in the given question we have convex mirror. And here X-axis is the principal axis and Y-axis is the pole of the mirror. Now we know that the ray travelling parallel to the axis gets reflected and passes from the focus. But here the given mirror is a convex mirror and it will diverge after reflecting and the extended line will pass from the focus.
Now for the parabola having equation y2=4ax, the focus is given by the coordinates (a,0). So for the given parabolic mirror focus will be at (a,0) and the extended line for the reflected ray will pass from the (a,0). The given diagram can we redrawn as
MN is the reflected ray and F is the focus. M is the point of intersection where the incident ray and parabolic mirror intersect and its abscissa was given 4a (abscissa is the X coordinate for the point M). We can find the Y-coordinate for point M by substituting the value of x in the parabolic equationy2=4ax. (Value of x is the 4a)
Hence we can write
