Question
Question: Figure shows a modified Fresnel biprism experiment with monochromatic source of wavelength\(500nm\)....
Figure shows a modified Fresnel biprism experiment with monochromatic source of wavelength500nm. The refracting angle of the prism is2∘. Find the fringe width.
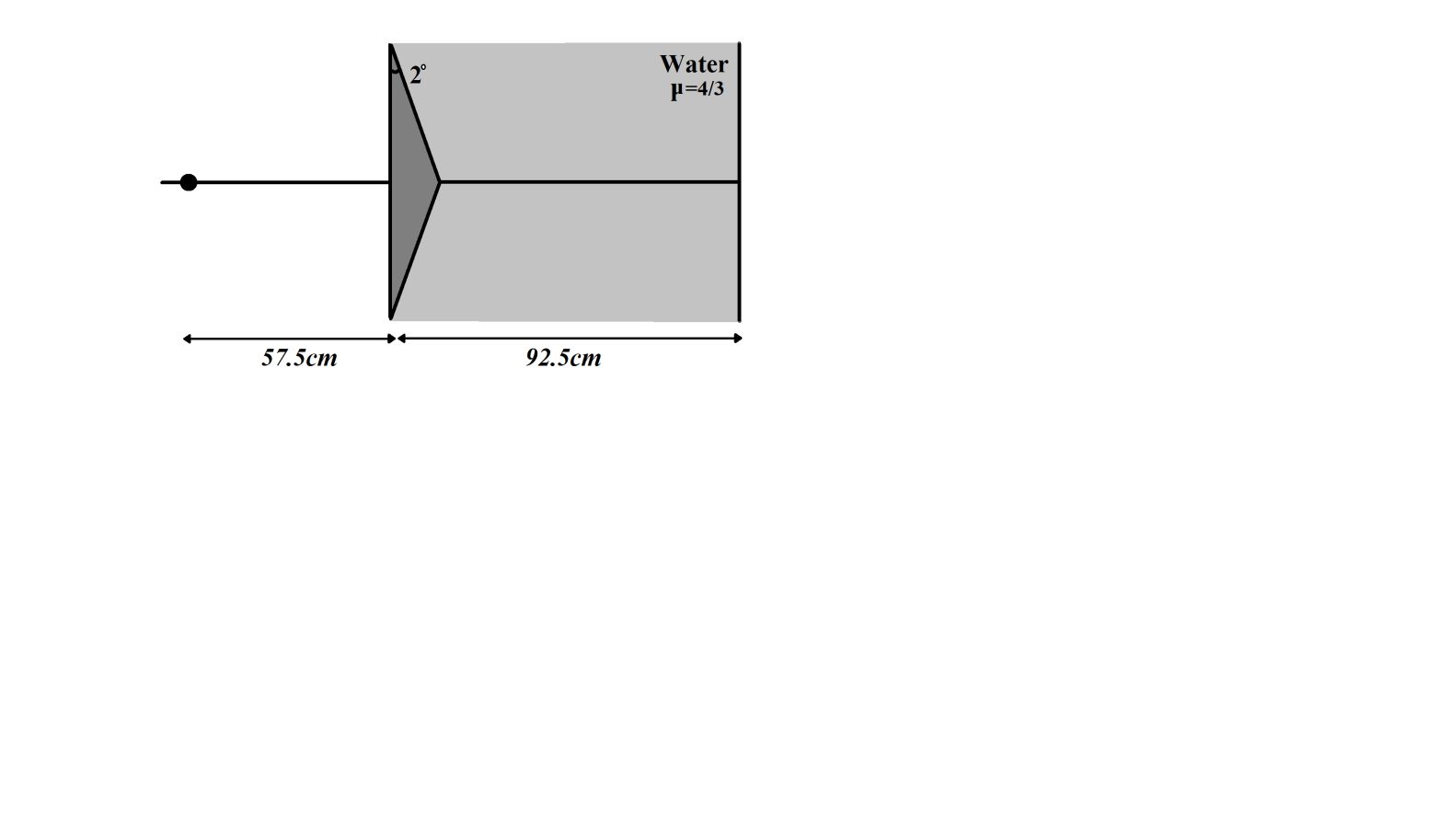
A. 0.1125mmB. 0.125mmC. 0.15mmD. 0.3mm
Solution
Hint: When a monochromatic light source is kept in front of biprism, two coherent virtual sources are produced. Fringe width is described as the distance between two consecutive dark fringes or two consecutive bright fringes obtained on the screen. We will use the expression for fringe width relating the wavelength of incident light, distance between the coherent sources and distance between the source and the screen.
Formula used:
Fringe width, β=dλD
Angle of deviation of prism with water on one side is, δ=A(μg−μ)
Distance between the sources, d=2δl
Complete step by step solution :
Fresnel biprism is an optical device for producing interference of light waves. It can be formed by joining base to base two thin prisms of very small refracting angles.
When a monochromatic light source is kept in front of biprism, two coherent virtual sources are produced. Interference fringes are obtained on the screen placed behind the prism. Interference pattern is observed on a limited region of the screen.
Fringe width is described as the distance between two consecutive dark fringes or two consecutive bright fringes obtained on the screen.
Fringe width is given as,
β=dλD
Where,
βis the fringe width
Dis the distance between the slit and screen
dis the distance between the sources
We are given a Fresnel biprism having refracting angle2∘. Monochromatic source has wavelength500nm.
Refractive index of glass, μg=1.5
Angle of deviation of prism with water on one side is,
δ=A(μg−μ)
Where,
Ais the angle of prism
μgis the refractive angle of glass
μis the refractive index of water
Putting values ofA, μgand μm
A=1802μg=23μm=34
δ=1802×722(23−34)δ=1802×722×61δ=90×7×311
Now,
d=2δl
Where,
d is the distance between the sources
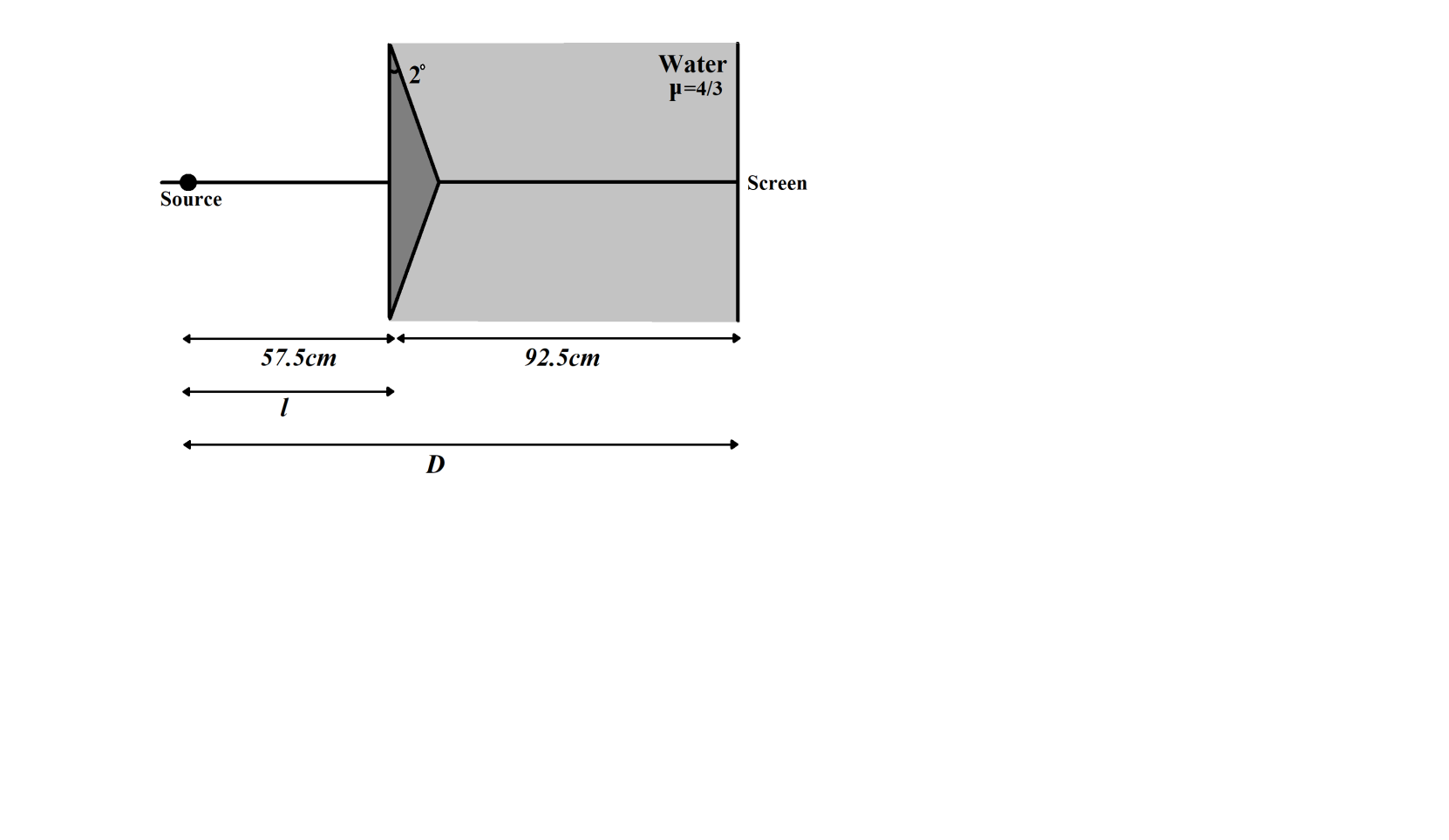
lis the distance between source and fresnel prism
Putting values of δand l
δ=90×7×311l=57.5cm=0.575m
d=2×(90×3×711)×0.575d=90×3×711×1.15d=18×3×711×0.23
Now,
Fringe width is given as,
β=dλD
Where,
βis the fringe width
λis the wavelength of incident light
Dis the distance between the sources and the screen
d is the distance between the sources
Putting values,
