Question

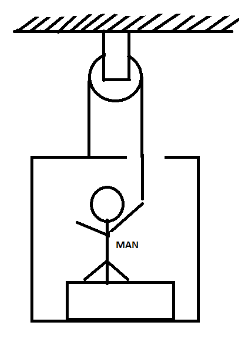
Figure shows a man of mass $60Kg$ standing on a light weighing machine dept in a box of mass $30kg$. The box is hanging from a pulley fixed to the ceiling through a light rope, the other end of which is held by the man himself. If the man manages to keep the box at rest, what is the weight shown by the machine? What force should he exert on the rope to get his correct weight on the machine.

Answer 1

In this question we are provided that the box is hanging with a pulley and the other end of the pulley is having a man who is standing inside that box as shown in the diagram. We have to calculate the weight of the machine and the force applied to the rope to measure the correct reading for that we have to form the force equations for both man and the box. And by equating the two conditions we can get our answer.

Complete step by step answer:
We are given that mass of the man (m)= $60kg$ and we are provided with the situation that the man is standing in a box connected with a pulley and we have to calculate the weight on the machine. For that we are considering that the tension experienced by the rope be T. and the weight on the man acting downward be mg where g is the acceleration due to gravity and the apparent weight on the man be represented by R’.

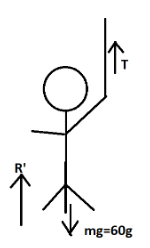
Hence, $R' + T - 60g = 0$ $\ldots \left( 1 \right)$
Now, mass of box (${m_b}$) =$30kg$ in this case the apparent weight will act upward, the condition will be

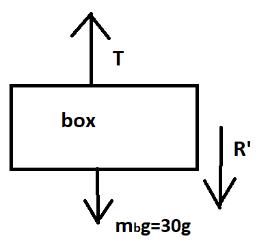
$T - R' - 30g = 0$ $\ldots \left( 2 \right)$
Equating the above marked equations
60g - R' - R' - 30g = 0 \\\ \Rightarrow 2R' = 30g \\\ \Rightarrow R' = 15g \\\
Hence, the weight shown by the machine is $15g$. Now, calculating the force due to correct weight on the machine. Let the box is experiencing upward force with acceleration a, and the force be taken as T’

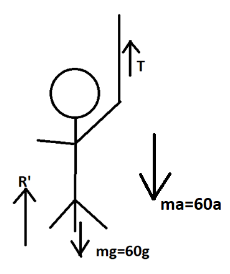
T' + R - 60g - 60a = 0 \\\ \Rightarrow T' + 60g - 60g - 60a = 0\left( {\because R = 60g} \right) \\\ \Rightarrow T' = 60a \\\ $\ldots \left( 3 \right)$
Now, taking the case for box which is accelerating downwards

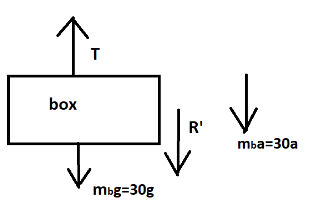
T' - R - 30g - 30a = 0 \\\ \Rightarrow T' - 60g - 30g - 30a = 0\left( {\because R = 60g} \right) \\\ \Rightarrow T' = 30a + 90g \\\ $\ldots \left( 4 \right)$
Equating $3,4$ equations while taking $g = 10m{s^{ - 2}}$
$60a = 30a + 90g \\\ \Rightarrow 30a = 90 \times 10 \\\ \Rightarrow a = 30$
And, using $3$
T' = 60a \\\ \therefore T' = 60 \times 30 = 1800N \\\
Hence, the force applied to the rope to have correct reading is $1800N$.

Note: We can take the value of acceleration due to gravity to be $9.8m{s^{ - 2}}$ but for our convenience we are taking $10m{s^{ - 2}}$. The answers for both the cases will be correct. The units should be written with full attention. Sometimes we are provided with milli or micro values which should be converted before solving.