Question

Figure shows a liquid flowing through a tube at the rate of $0.1{m^3}/s$. The tube is branched into two semi-circular tubes of cross-sectional area $A/3$(upper) and $2A/3$(lower). The velocity of liquid at Q is (the cross section of main tube is $A = {10^{ - 2}}{m^2}$ and ${v_P} = 20m/s$)

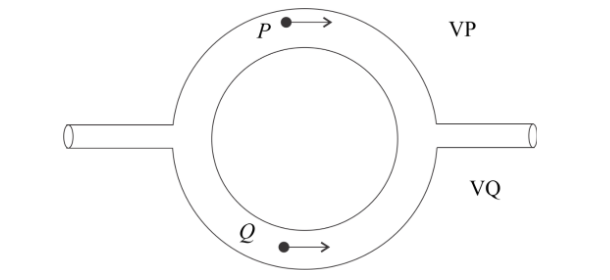
(A) $5m/s$
(B) $30m/s$
(C) $35m/s$
(D) None of the above

Answer 1

Hint Volume of liquid pass through the main tube per second is equal to sum of volume of liquid pass through the both semi-circular tubes per second. We know that the volume of liquid passing through a cross section in one second is a product of the cross-sectional area and speed of liquid. We just find the rate of flow in P and Q, and equate then with the rate of flow of the main tube.

Complete step by step solution
The rate of flow of liquid in the main tube is $0.1{m^3}/s$ and area of the main tube is $A = {10^{ - 2}}{m^2}$.
Let ${v_P}$ and ${v_{\text{Q}}}$ are velocities of liquid in tube P and Q respectively.
As given ${v_P} = 20m/s$.
Cross sectional area of tube P and Q is $A/3$ and $2A/3$ respectively.
Rate of flow of liquid in tube P is ${R_P} = {v_p} \times \dfrac{A}{3} = \dfrac{{20A}}{3}{m^3}/s$.
Rate of flow of liquid in tube Q is ${R_{\text{Q}}} = {v_{\text{Q}}} \times \dfrac{{2A}}{3}{m^3}/s$

We know that the rate of flow of the main tube is equal to the sum of the rate of flow of tube P and Q.
Then, $\dfrac{{20A}}{3} + \dfrac{{2A{v_{\text{Q}}}}}{3} = 0.1$ or $20A + 2A{v_{\text{Q}}} = 0.3$
${v_{\text{Q}}} = \dfrac{{0.3 - 20A}}{{2A}}$
Putting value of A in above equation, we get
${v_{\text{Q}}} = \dfrac{{0.3 - 20 \times 0.01}}{{2 \times 0.01}} = \dfrac{{0.3 - 0.2}}{{0.02}} = 5m/s$

Hence the correct answer is option A.

Note: For a junction of liquid flow pipes, liquid entered at the junction is equal to liquid leaving the junction. Here liquid enters at the main junction and liquid enters from the main tube and liquid leaves the junction and flows in tube P and Q as shown in figure.