Question

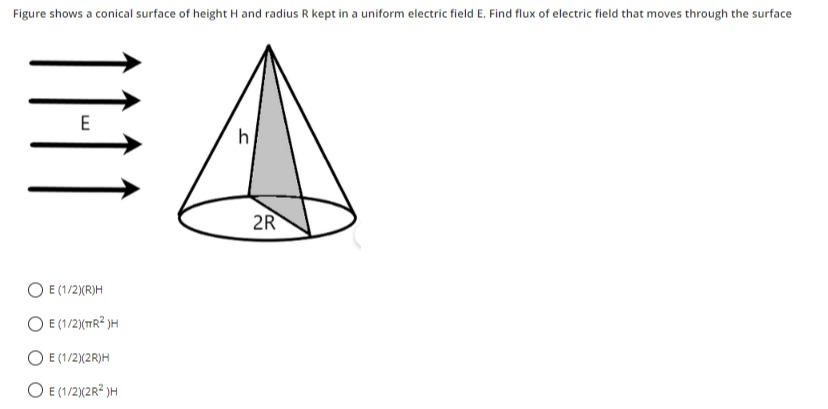
Figure shows a conical surface of height H and radius R kept in a uniform electric field E. Find flux of electric field that moves through the surface

• A. E (1/2)(R)H
• B. Ε (1/2) ($\pi$R$^2$)H
• C. E (1/2)(2R)H
• D. E (1/2)(2R$^2$ )H

Answer 1

Answer: (C)

E (1/2)(2R)H

Answer 2

The electric flux ($\Phi$) through a surface is given by the dot product of the electric field vector ($\vec{E}$) and the area vector ($d\vec{A}$), integrated over the surface:

$\Phi = \int \vec{E} \cdot d\vec{A}$

For a uniform electric field $\vec{E}$ and a surface whose projection perpendicular to the field has area $A_{proj}$, the flux is simply:

$\Phi = E \cdot A_{proj}$

In this problem, a conical surface of height H and radius R is placed in a uniform electric field E, which is parallel to its base.

1. Flux through the circular base: The electric field lines are parallel to the base of the cone. The area vector for the base is perpendicular to the base. Therefore, the angle between the electric field and the area vector of the base is 90 degrees. Since $\cos(90^\circ) = 0$, the electric flux through the circular base of the cone is zero.

2. Flux through the curved conical surface: The electric field lines pass through the curved surface of the cone. To find the flux through this curved surface, we consider its effective cross-sectional area perpendicular to the electric field. Imagine viewing the cone from the direction of the electric field (i.e., looking along the horizontal direction of E). The shape that the cone projects onto a plane perpendicular to the electric field is a triangle. The base of this projected triangle is the diameter of the cone's base, which is $2R$. The height of this projected triangle is the height of the cone, which is $H$.

   The area of this projected triangle ($A_{proj}$) is:

   $A_{proj} = \frac{1}{2} \times \text{base} \times \text{height}$

   $A_{proj} = \frac{1}{2} \times (2R) \times H$

   $A_{proj} = RH$

   Since the electric field is uniform and perpendicular to this projected area, the electric flux through the curved conical surface is:

   $\Phi = E \cdot A_{proj}$

   $\Phi = E \cdot (RH)$

   The calculated flux $E R H$ matches option C.