Question
Question: Figure shows a composite system of two uniform rods of lengths as indicated. If both the rods are of...
Figure shows a composite system of two uniform rods of lengths as indicated. If both the rods are of same density, then the coordinates of the center of mass of the system of rods are:
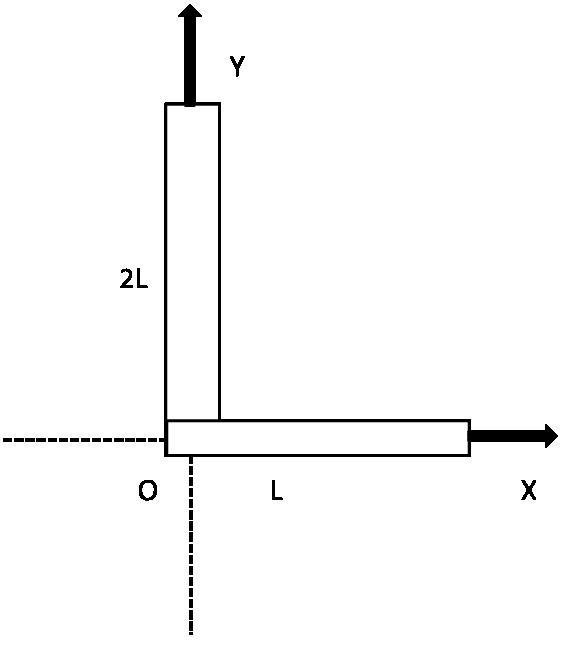
A) (2L,32L)
B) (4L,32L)
C) (6L,32L)
D) (6L,3L)
Solution
According to the given question, we need to find the coordinates of the centre of mass of the system. For that first we need to find the centre of mass of both the rods separately and then the coordinates of the line joining their centre of mass.
Complete step by step solution:
As we can see from the figure, that the rod on Y axis is twice in length of the rod on X axis. Since both the rods are of the same density so their mass will change according to their length.
Now, let us assume the mass of rod on X axis be M
Then the mass of the rod on the Y axis will be 2M, since the rods are of the same density.
i.e. m1=Mand m2=2M
We know that the centre of mass of a uniformly distributed rod is at its centre or mid-point.
Therefore, the centre of mass of the rod on the X axis will be at 2L as the length of the rod is L.
Similarly, the centre of mass of the rod on the Y axis will be at L as the length of the rod is 2L.
Now, the coordinates of the centre of mass of rod on X axis will be (2L,o) i.e. x1=2L,y1=0
And the coordinates of the centre of mass of rod on Y axis will be (0,L)i.e. x2=0,y2=L
As we know that, for coordinates of centre of mass,
Xcm=m1+m2m1x1+m2x2……………………..(i)
Ycm=m1+m2m1y1+m2y2……………………….(ii)
Now we will put the values of x, y and m in equation (i) and (ii)
Xcm=m1+m2m1x1+m2x2
⇒M+2MM×2L+2M×0=3M×2ML=6L
Ycm=m1+m2m1y1+m2y2
⇒M+2MM×0+2M×L=3M2ML=32L
Hence, option (C) is correct with centre of mass of the system as (6L,32L).
Note: We need to remember the position of centre of mass for different dimensions to get correct solutions. Also, for finding the centre of mass for the entire system, we need to find the centre of mass for each dimension separately and then approach the entire system.
