Question

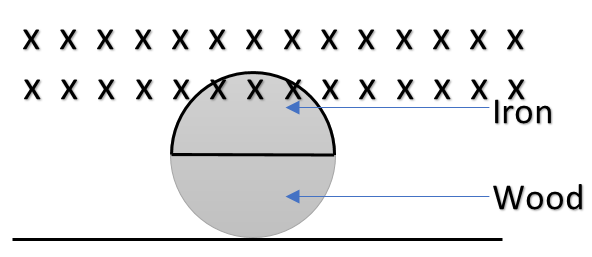
Figure shows a circular wheel of radius 10 cm whose upper half is made of iron and lower half of wood. The two junctions are joined by an iron rod. Uniform magnetic fields $B = 2\times 10^{-4} T$ exist in space shown. The wheel is set in pure rolling. If it takes 2 s for the iron part to come down and wooden part to go up, then the average induced emf during this period is:

$\text{A.}\quad 1.57 \times 10^{-6} V$
$\text{B.}\quad 1.5 \times 10^{-7} V$
$\text{C.}\quad 15.7 \times 10^{-6} V$
$\text{D.}\quad 1.55 \times 10^{-8} V$

Answer 1

According to Faraday’s law, if there is a change in flux in a coil, it will produce or generate an E.M.F. in the coil. According to Lenz law, the change in magnetic field is opposed in such a manner that the current inside the coil will resist the magnetic field by flowing in a particular direction.
Formula used:
$\phi = BA,|\ E| = \dfrac{d\phi}{dt}$

Complete answer:
As wood is an insulator, thus when the wood part is going into the magnetic field, no current will flow through the wooden frame, due to its higher resistance. Now that we know only through iron frames, the current will flow, thus we can say that the flux is changing continuously because the area in contact with the field is changing continuously. Hence using Faraday’s law, the emf generated will be:
$E = \dfrac{d\phi}{dt}$ [For magnitude only]
Also $\phi = BA$
Hence differentiating the flux equation wrt time, we get;
$E = \dfrac{d(BA)}{dt} = B\dfrac{dA}{dt}$
Hence it will only depend upon the rate of change of area.
Now, let a conducting frame of the shape of a semicircle enter a region of uniform magnetic field (above the blue line as shown in the figure).

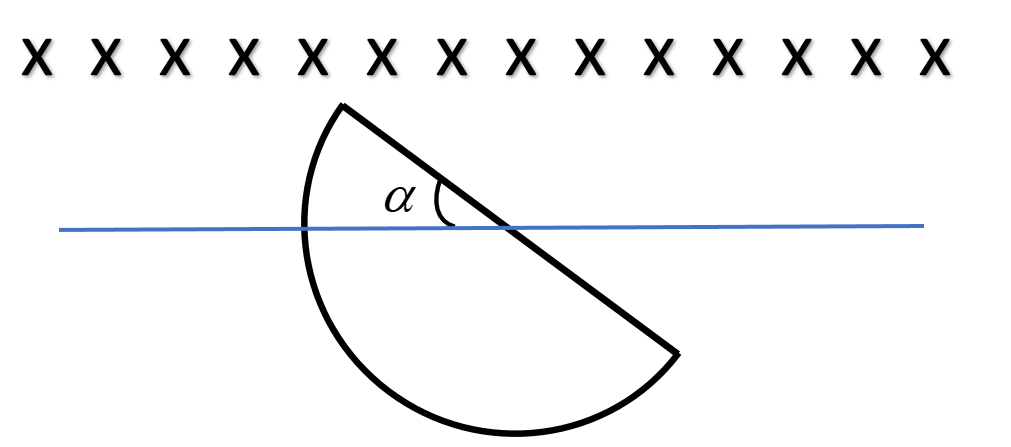
Let at an instant, it makes an angle$\alpha$with the magnetic field. Hence the area entered the magnetic field is given by:
$A = \dfrac12 \alpha r^2$
But $E = \dfrac{BdA}{dt}$
Thus$\dfrac{dA}{dt} = \dfrac12 \dfrac{d\alpha}{dt}r^2 = \dfrac{1 }{2}\omega r^2$, where $\omega$ is the angular velocity at that instant.
Also given that it takes 2 s for the iron part to come down and wooden part to go up, hence the loop turns by $\pi$ radian in 2 s.
Hence the angular velocity of loop is $\dfrac{\pi}{2}rad \ s^{-1}$
Thus $\dfrac{dA}{dt} = \dfrac{1}{2} \times \dfrac{\pi}{2} \times r^2$
Hence $E = \dfrac{BdA}{dt}$
$E = \dfrac{\pi Br^2}{4}$
Hence putting values of magnetic field and radius, we get;
$E = \dfrac{3.14 (2\times 10^{-4})(0.1)^2}{4} = 1.57\times 10^{-6} V$

So, the correct answer is “Option A”.

Note:
In the question, we are asked to find the average E.M.F, why so? This is because according to Lenz law, whenever there is a change in magnetic flux, the body or loop will oppose the change. Hence the angular velocity of the loop must decrease with time. But since we didn’t consider this effect, the value is approximate.