Question
Question: Figure shows a charge array known as an electric quadrupole. For a point on the axis of the quadrupl...
Figure shows a charge array known as an electric quadrupole. For a point on the axis of the quadruple, obtain the dependence of potential on r for r/a>>1, and contrast your results with that due to an electric dipole, and an electric monopole (i.e., a single charge).
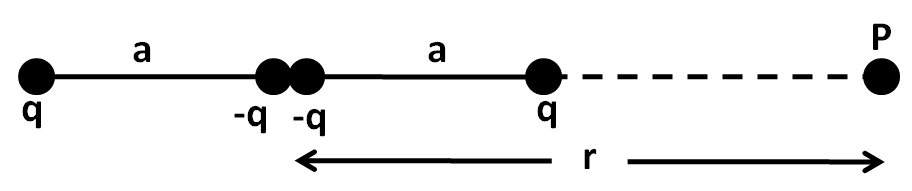
Solution
To solve this question, we need to use the formula for the potential at a point due to a point charge for calculating the potential due to all the four point charges. Then we have to make the comparison with the known formulas for the potential due to a dipole and a monopole.
Formula used: The formulae used in solving this question are given by
V=rKq, here V is the potential due to a point charge q at a distance of r.
V=r2Kp, here V is the potential due to an electric dipole of dipole moment p at an axial distance of r from its centre.
Complete step by step answer
Let us label the points as shown in the figure below.
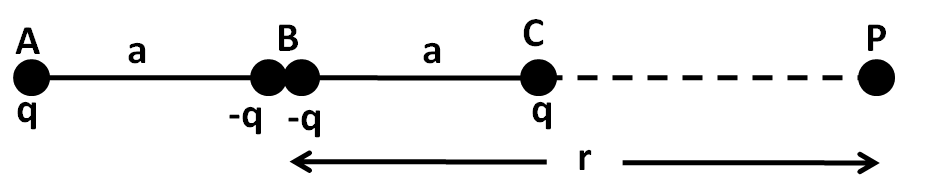
Since both the charges −q and −q at the point B, we can say that a total charge of −2q is present at B. So we can redraw the above figure as

We can observe from the above figure that AP=r+a, BP=r, and CP=r−a.
We know that the potential due to a point charge is given by
⇒V=rKq …………………….(1)
So the potential at the point P due to the charge at A is
⇒VA=APKq
⇒VA=r+aKq …………………….(2)
Similarly, the potential due to the charges at B and C at P are respectively,
⇒VB=r−2Kq …………………….(3)
⇒VC=r−aKq …………………….(4)
So the net potential at the point P is
⇒V=VA+VB+VC
From (2) (3) and (4) we have
⇒V=r+aKq+r−2Kq+r−aKq
Taking Kq common, we get
⇒V=Kq(r+a1−r2+r−a1)
Taking the LCM we have
⇒V=Kq((r+a)r(r−a)r(r−a)−2(r+a)(r−a)+r(r+a))
⇒V=Kq((r+a)r(r−a)r2−ar−2r2+2a2+r2+ar)
On simplifying, we get
⇒V=Kq((r+a)r(r−a)2a2)
⇒V=r(r2−a2)2Kqa2
Taking r2 common from the denominator, we have
⇒V=r3(1−a2/r2)2Kqa2
According to the question, r/a>>1. This means a2/r2≈0. So from above we get
⇒V=r32Kqa2
This is the potential due to the electric quadrupole.
⇒V∝r31
Also we know that for an electric dipole, the axial potential is given by
⇒V=r2Kp
So that
⇒V∝r21
Finally, the potential due to a point charge is given by
⇒V=rKq
This means that
⇒V∝r1
Hence, the potential due to a monopole, a dipole, and a quadruple is inversely proportional to the first, second and third power of distance respectively.
Note
We could also divide the given quadruple into two adjacent dipoles and apply the formula of the electric potential for both of the dipoles at the point P. Then on adding these two potentials we will get the required value of the net potential at the point.
