Question

Figure shows a block placed on a bracket. Bracket is placed on a smooth floor, it is pulled by a force F=6N horizontally. Block is projected with velocity $v_0$ relative to bracket as shown in figure. Find time in second after which it stops relative to bracket. Horizontal surface of bracket is smooth while vertical surface is rough (Given: m=1kg, M=5kg, $v_0$=4m/s $\mu$=0.5), the motion of bracket is restricted in z-direction.

Answer 1

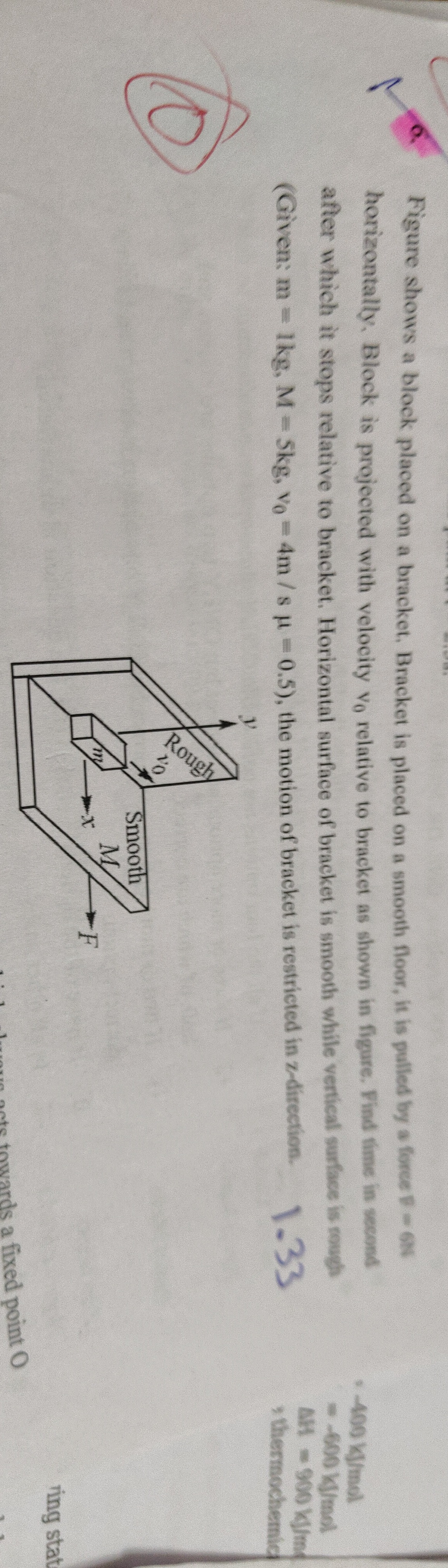
8

Answer 2

The problem involves analyzing the motion of a block relative to a bracket, which itself is accelerating. We will use Newton's laws of motion and kinematic equations.

1. Analyze the motion in the x-direction (direction of force F): Let $a_M$ be the acceleration of the bracket (M) and $a_m$ be the acceleration of the block (m) in the x-direction. The bracket is pulled by a force F. The block is in contact with the vertical rough surface of the bracket. Since the horizontal surface of the bracket is smooth, there is no friction between the block's bottom and the bracket's floor. The block will accelerate along with the bracket in the x-direction, assuming it remains in contact with the vertical wall. Therefore, $a_m = a_M$.

• For the block (m) in x-direction: The normal force ($N_x$) from the vertical wall provides the acceleration to the block. $N_x = m a_m = m a_M$ (Equation 1)

• For the bracket (M) in x-direction: The applied force F acts on the bracket. The block exerts a reaction force ($N_x$) on the bracket in the opposite direction. $F - N_x = M a_M$ (Equation 2)

Substitute Equation 1 into Equation 2: $F - m a_M = M a_M$ $F = (M+m) a_M$ The acceleration of the bracket (and the block in x-direction) is: $a_M = \frac{F}{M+m}$

Given: F = 6 N, m = 1 kg, M = 5 kg. $a_M = \frac{6 \text{ N}}{1 \text{ kg} + 5 \text{ kg}} = \frac{6 \text{ N}}{6 \text{ kg}} = 1 \text{ m/s}^2$.

Now, calculate the normal force $N_x$: $N_x = m a_M = 1 \text{ kg} \times 1 \text{ m/s}^2 = 1 \text{ N}$.

2. Analyze the motion in the y-direction (direction of initial relative velocity $v_0$): The block is projected with an initial velocity $v_0$ relative to the bracket in the y-direction. The vertical surface is rough, so it exerts a kinetic friction force on the block, opposing its motion. The friction force $f_k = \mu N_x$.

Given: $\mu = 0.5$. $f_k = 0.5 \times 1 \text{ N} = 0.5 \text{ N}$.

This friction force acts on the block in the -y direction (opposite to $v_0$). The bracket itself does not move in the y-direction. Therefore, the acceleration of the block in the y-direction ($a_y$) is also its relative acceleration with respect to the bracket in the y-direction ($a_{rel,y}$).

• For the block (m) in y-direction: $-f_k = m a_y$ $-0.5 \text{ N} = 1 \text{ kg} \times a_y$ $a_y = -0.5 \text{ m/s}^2$.

3. Calculate the time until the block stops relative to the bracket: The initial velocity of the block relative to the bracket in the y-direction is $v_0 = 4 \text{ m/s}$. The final relative velocity in the y-direction is 0 m/s (when it stops relative to the bracket). The acceleration of the block relative to the bracket in the y-direction is $a_{rel,y} = a_y = -0.5 \text{ m/s}^2$.

Using the kinematic equation: $v_{final} = v_{initial} + a_{rel} t$ $0 = v_0 + a_y t$ $0 = 4 \text{ m/s} + (-0.5 \text{ m/s}^2) t$ $0.5 t = 4$ $t = \frac{4}{0.5} = 8 \text{ s}$.

The time after which the block stops relative to the bracket is 8 seconds.