Question

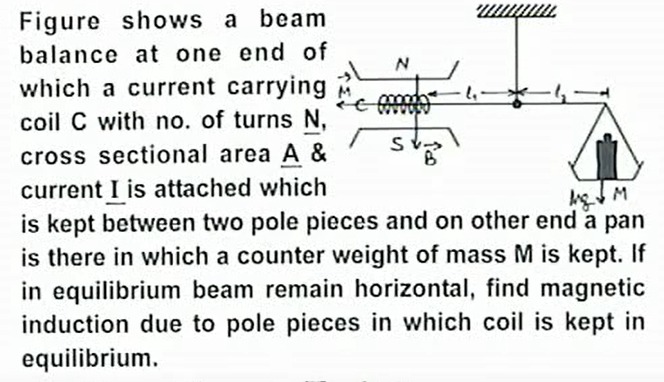
Figure shows a beam balance at one end of which a current carrying coil C with no. of turns $\underline{N}$, cross sectional area $\underline{A}$ & current $\underline{I}$ is attached which is kept between two pole pieces and on other end a pan is there in which a counter weight of mass M is kept. If in equilibrium beam remain horizontal, find magnetic induction due to pole pieces in which coil is kept in equilibrium.

Answer 1

$\frac{Mg l_2}{NIAl_1}$

Answer 2

The beam balance is in equilibrium when the torques on both sides of the pivot are balanced. The coil is at a distance $l_1$ from the pivot, and the counterweight of mass M is at a distance $l_2$. The weight of the counterweight is $Mg$. The magnetic force on the coil, let's call it $F_{mag}$, acts at a distance $l_1$ from the pivot. For equilibrium, the torque due to the magnetic force must balance the torque due to the weight. Assuming the magnetic force $F_{mag}$ acts upwards to counteract the weight on the other side: $F_{mag} \cdot l_1 = Mg \cdot l_2$

The magnetic force on a current-carrying coil in a magnetic field is given by $F_{mag} = NIAB$, where N is the number of turns, I is the current, A is the cross-sectional area, and B is the magnetic induction. Assuming this formula for the magnetic force: $NIAB \cdot l_1 = Mg \cdot l_2$

We are asked to find the magnetic induction B. Rearranging the equation to solve for B: $B = \frac{Mg \cdot l_2}{NIAl_1}$