Question

Figure shows a $5kg$ ladder hanging from a string that is connected to the ceiling and is having a spring balance connected in between. A boy of mass $25kg$ is climbing up the ladder at acceleration $1m\,{{s}^{-2}}$. Assuming the spring balance and the string to be massless and the spring to show a constant reading, the reading of spring balance is:

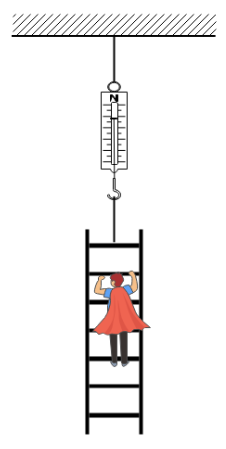
(A). $30kg$
(B). $32.5kg$
(C). $35kg$
(D). $37.5kg$

Answer 1

The spring balance will calculate the collective weight of ladder and boy. Newton's second law states that force is required to change the state of rest or motion of an object. Consider the boy and ladder as separate systems and calculate the forces acting on each system as the other forces will affect the overall effect of weight on each body. Hence, calculate their collective weight which will also be the tension in the string.

Formulas used:
$N'-mg=ma$
$N'+mg-T=0$

Complete step-by-step solution:
The FBD diagram of the system is as shown

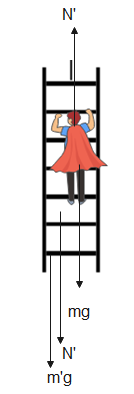
Let us consider the forces acting on the man,
$N'-mg=ma$ - (1)
Here, $N'$ is the normal reaction acting on the man
$mg$ is the gravitational force
$ma$ is the overall force acting on him

Substituting values in eq (1), we get,
$\begin{aligned} & N'-25\times 10=25\times 1 \\\ & \Rightarrow N'=275\,N \\\ \end{aligned}$

Now, the forces acting on the ladder are,
$N'+m'g-T=0$ - (2)
Here, $m'$ is the mass of the ladder
Here, $T$ is the tension in the string

Substituting values in eq (2), we get,
$\begin{aligned} & \Rightarrow T=275+50 \\\ & \therefore T=325N \\\ \end{aligned}$

The spring balance will weigh the weight of the ladder and mass collectively. Therefore,
$\begin{aligned} & T=m''g \\\ & \Rightarrow 325=m'\times 10 \\\ & \therefore m'=32.5kg \\\ \end{aligned}$

The reading on spring balance will be- $32.5kg$. Hence, the correct option is (B).

Additional Information:
The normal force acting between two surfaces is a force which prevents the surfaces from passing through each other. Its direction is always perpendicular to the surfaces. Normal reactions are equal in magnitude but opposite in direction and are always repulsive in nature.

Note:
The spring balance does not weigh mass but weight of an object. It works on the principle that the force required to stretch the spring of spring balance is directly proportional to the distance through which it needs to stretch. The spring constant is calculated by dividing the force by the reading on spring balance.