Question
Question: Figure shown a part of an electric circuit, The potentials at the points a, b, and c are \[30V,12V\]...
Figure shown a part of an electric circuit, The potentials at the points a, b, and c are 30V,12V, and 2V respectively. Find the currents through the three resistors.
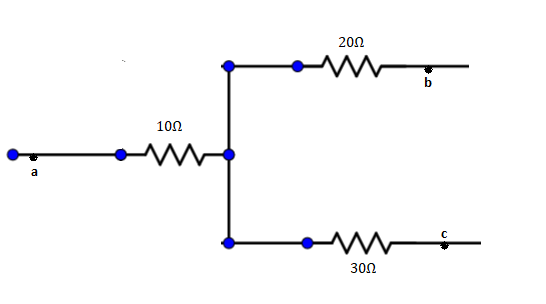
Solution
When resistors are connected adjacently in a serial manner, then the circuit will be known as resistor in serial connection. In a serial circuit the same current flows through the resistors. As the resistors connect serially then the common current passes through each resistor and total resistance will be RT.
RT=R1+R2+R3 ….
When resistors are connected in a parallel manner, then the circuit is called as resistors in parallel connection. In this parallel circuit current takes multiple paths to flow in the circuit. The reciprocal resistance of all resistance added together to give reciprocal values of equivalent total resistance.
Rn1=R11+R21+R31+......
Formula used:
i1=i2+i3
Complete step by step answer:
Let the potential will be Xv
From the figure, ia=10Va−V0
By putting Va=30V,V0=X
So, ia=1030−X
Similarly,
ib=20V0−Vb
⇒20X−12
Also,
i3=30V0−VC
⇒30X−2
From Kirchhoff’s junction law,
i1=i2+i3
1030−X=20X−12+30X−2
By dividing the denominators by 10
30−X=2X−12+3X−2
By taking LCM
30−X=63X−36+2X−4
Bringing 6 to LHS and multiply
180−6X=5X−40
Bringing X values one side and constant values other side.
X=11220=20V
i1=1030−20=1A
i2=2020−12=0.4A
i3=3020−2=0.6A
The current through the three resistors are 1A,0.4A,0.6A.
Note: The resistors are used to reduce current flows in the circuit.
Characteristic of resistors are,
1. Low temperature coefficient of resistance
2. Power rating
3. Electrical resistivity of the material
4. Insulation of the wires

