Question

Figure show a hemispherical shell having uniform mass density. The direction of gravitational field intensity at point P will be along:

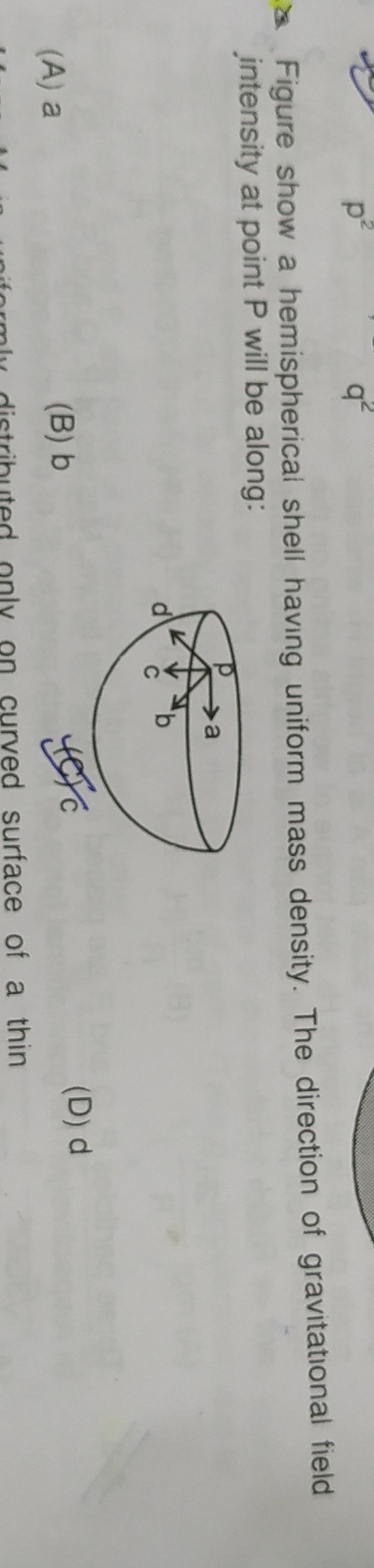
• A. a
• B. b
• C. c
• D. d

Answer 1

Answer: (B)

b

Answer 2

The question asks for the direction of gravitational field intensity at point P, which is the center of the base of a hemispherical shell with uniform mass density.

1. Understanding Gravitational Field Intensity: Gravitational field intensity ($\vec{E}$) at a point is the gravitational force experienced by a unit mass placed at that point. It is a vector quantity and always points towards the source of the mass.

2. Symmetry Argument:

   • The hemispherical shell has uniform mass density and is symmetric about the vertical axis passing through its apex and the center of its base (point P).
   • Consider any small mass element dm on the hemispherical shell. It will create a gravitational field dE at point P, directed from P towards dm.
   • Resolve this dE into two components: one along the axis of symmetry (vertical component) and one perpendicular to the axis of symmetry (horizontal component).
   • For every mass element dm on one side of the axis of symmetry, there is a symmetrically identical mass element dm' on the opposite side.
   • The horizontal components of dE and dE' due to these symmetric mass elements will be equal in magnitude and opposite in direction. Therefore, they will cancel each other out.
   • The vertical components of dE and dE' will both point upwards (towards the mass of the hemisphere) and will add up.

3. Net Direction: Since all horizontal components cancel out due to symmetry, the net gravitational field intensity at P will only have a vertical component. As all the mass of the hemispherical shell is located above the plane of the base (where P is located), the gravitational force (and thus the field intensity) will be directed upwards, towards the bulk of the mass of the hemisphere.

4. Matching with Options: In the given figure:

   • Arrow 'a' points downwards, away from the hemisphere.
   • Arrow 'b' points vertically upwards, into the hemisphere.
   • Arrows 'c' and 'd' point horizontally.

   Based on our analysis, the gravitational field intensity at P must be vertically upwards, towards the mass. This corresponds to direction 'b'.