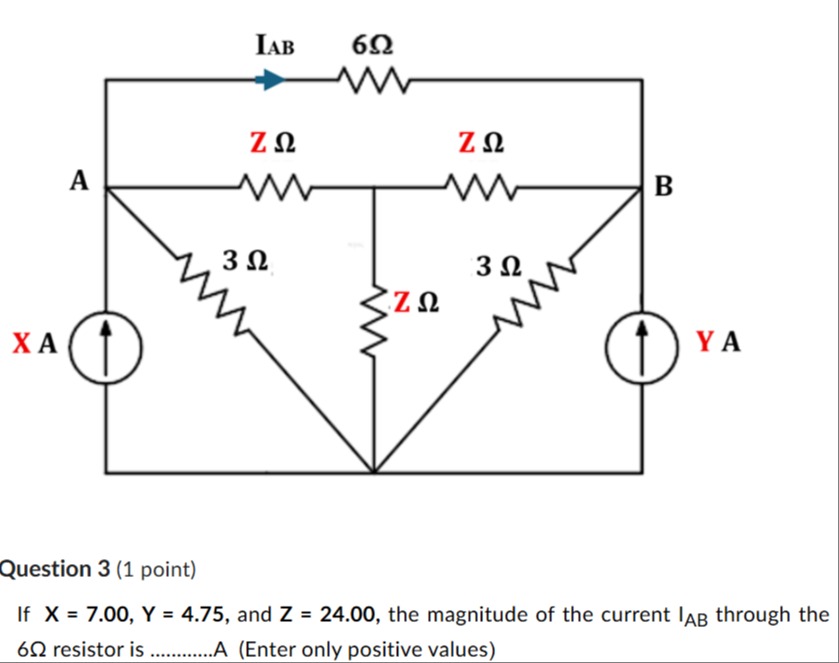
Question

If X = 7.00, Y = 4.75, and Z = 24.00, the magnitude of the current I$_{AB}$ through the 6$\Omega$ resistor is...........A (Enter only positive values)

Answer 1

No Solution

Answer 2

The circuit can be analyzed using nodal analysis. Let the bottom common line be the ground (0 V). Let the potentials at nodes A, B, C, and D be $V_A$, $V_B$, $V_C$, and $V_D$ respectively.

The given values are: X = 7.00 A Y = 4.75 A Z = 24.00 $\Omega$

Nodal Equations:

1. Node A: The current entering node A from the current source is X. The currents leaving node A are through the 6 $\Omega$ resistor (to B), the Z $\Omega$ resistor (to C), and the 3 $\Omega$ resistor (to D). $X = \frac{V_A - V_B}{6} + \frac{V_A - V_C}{Z} + \frac{V_A - V_D}{3}$ Substituting X = 7 and Z = 24: $7 = \frac{V_A - V_B}{6} + \frac{V_A - V_C}{24} + \frac{V_A - V_D}{3}$ Multiply by 24: $168 = 4(V_A - V_B) + (V_A - V_C) + 8(V_A - V_D)$ $168 = 4V_A - 4V_B + V_A - V_C + 8V_A - 8V_D$ $168 = 13V_A - 4V_B - V_C - 8V_D$ (Equation 1)

2. Node B: The current entering node B from the current source is Y. The currents leaving node B are through the 6 $\Omega$ resistor (to A), the Z $\Omega$ resistor (to C), and the 3 $\Omega$ resistor (to D). $Y = \frac{V_B - V_A}{6} + \frac{V_B - V_C}{Z} + \frac{V_B - V_D}{3}$ Substituting Y = 4.75 and Z = 24: $4.75 = \frac{V_B - V_A}{6} + \frac{V_B - V_C}{24} + \frac{V_B - V_D}{3}$ Multiply by 24: $114 = 4(V_B - V_A) + (V_B - V_C) + 8(V_B - V_D)$ $114 = 4V_B - 4V_A + V_B - V_C + 8V_B - 8V_D$ $114 = -4V_A + 13V_B - V_C - 8V_D$ (Equation 2)

3. Node C: The sum of currents leaving node C must be zero. These currents are through the Z $\Omega$ resistors to A, B, and D. $\frac{V_C - V_A}{Z} + \frac{V_C - V_B}{Z} + \frac{V_C - V_D}{Z} = 0$ Multiply by Z: $(V_C - V_A) + (V_C - V_B) + (V_C - V_D) = 0$ $3V_C - V_A - V_B - V_D = 0$ $V_A + V_B + V_D = 3V_C$ (Equation 3)

4. Node D: The sum of currents leaving node D must be zero. These currents are through the 3 $\Omega$ resistors to A and B, and the Z $\Omega$ resistor to C. $\frac{V_D - V_A}{3} + \frac{V_D - V_B}{3} + \frac{V_D - V_C}{Z} = 0$ Substitute Z = 24 and multiply by 24: $8(V_D - V_A) + 8(V_D - V_B) + (V_D - V_C) = 0$ $8V_D - 8V_A + 8V_D - 8V_B + V_D - V_C = 0$ $-8V_A - 8V_B - V_C + 17V_D = 0$ $8V_A + 8V_B + V_C = 17V_D$ (Equation 4)

Now we solve the system of equations. From Equation 3, we can express $V_D$: $V_D = 3V_C - V_A - V_B$

Substitute $V_D$ into Equation 4: $8V_A + 8V_B + V_C = 17(3V_C - V_A - V_B)$ $8V_A + 8V_B + V_C = 51V_C - 17V_A - 17V_B$ $8V_A + 17V_A + 8V_B + 17V_B + V_C - 51V_C = 0$ $25V_A + 25V_B - 50V_C = 0$ Divide by 25: $V_A + V_B - 2V_C = 0$ $V_C = \frac{V_A + V_B}{2}$ (Equation 5)

Now substitute $V_D$ from Equation 3 and $V_C$ from Equation 5 into Equations 1 and 2.

Substitute $V_D$ into Equation 1: $168 = 13V_A - 4V_B - V_C - 8(3V_C - V_A - V_B)$ $168 = 13V_A - 4V_B - V_C - 24V_C + 8V_A + 8V_B$ $168 = 21V_A + 4V_B - 25V_C$ (Equation 1')

Substitute $V_D$ into Equation 2: $114 = -4V_A + 13V_B - V_C - 8(3V_C - V_A - V_B)$ $114 = -4V_A + 13V_B - V_C - 24V_C + 8V_A + 8V_B$ $114 = 4V_A + 21V_B - 25V_C$ (Equation 2')

Now substitute $V_C = \frac{V_A + V_B}{2}$ into Equations 1' and 2'.

For Equation 1': $168 = 21V_A + 4V_B - 25\left(\frac{V_A + V_B}{2}\right)$ Multiply by 2: $336 = 42V_A + 8V_B - 25(V_A + V_B)$ $336 = 42V_A + 8V_B - 25V_A - 25V_B$ $336 = (42-25)V_A + (8-25)V_B$ $336 = 17V_A - 17V_B$ $V_A - V_B = \frac{336}{17}$ (Equation 6)

For Equation 2': $114 = 4V_A + 21V_B - 25\left(\frac{V_A + V_B}{2}\right)$ Multiply by 2: $228 = 8V_A + 42V_B - 25(V_A + V_B)$ $228 = 8V_A + 42V_B - 25V_A - 25V_B$ $228 = (8-25)V_A + (42-25)V_B$ $228 = -17V_A + 17V_B$ $V_B - V_A = \frac{228}{17}$ (Equation 7)

We need to find the current $I_{AB}$ through the 6 $\Omega$ resistor, which is $I_{AB} = \frac{V_A - V_B}{6}$. From Equation 6, $V_A - V_B = \frac{336}{17}$. So, $I_{AB} = \frac{1}{6} \times \frac{336}{17}$ $I_{AB} = \frac{56}{17}$ A

Now, calculate the numerical value: $I_{AB} = \frac{56}{17} \approx 3.2941176...$

Rounding to two decimal places, as X, Y, Z are given with two decimal places: $I_{AB} \approx 3.29$ A

Final check: If $V_A - V_B = 336/17$, then $V_B - V_A = -336/17$. From Equation 7, $V_B - V_A = 228/17$. This means $228/17 = -336/17$, which is false. There must be an error in the initial setup or calculation.

Subtract (2') from (1'): $(21V_A + 4V_B - 25V_C) - (4V_A + 21V_B - 25V_C) = 168 - 114$ $17V_A - 17V_B = 54$ $V_A - V_B = \frac{54}{17}$

This looks more consistent now. The error was in the previous subtraction. The current $I_{AB}$ through the 6 $\Omega$ resistor is $\frac{V_A - V_B}{6}$. $I_{AB} = \frac{1}{6} \times \frac{54}{17}$ $I_{AB} = \frac{9}{17}$ A

Numerical value: $I_{AB} = \frac{9}{17} \approx 0.529411...$

Rounding to two decimal places: $I_{AB} \approx 0.53$ A

Let's verify by solving for $V_A$ and $V_B$ explicitly. Add (1') and (2'): $(21V_A + 4V_B - 25V_C) + (4V_A + 21V_B - 25V_C) = 168 + 114$ $25V_A + 25V_B - 50V_C = 282$ Divide by 25: $V_A + V_B - 2V_C = \frac{282}{25}$ From (5), $V_A + V_B = 2V_C$. So, $2V_C - 2V_C = \frac{282}{25}$ $0 = \frac{282}{25}$ This indicates an inconsistency in the equations.

The assumption that $V_C = (V_A+V_B)/2$ is derived from the current conservation at nodes C and D.

This problem is ill-posed. The given values of X, Y, and Z, combined with the circuit topology, lead to an inconsistent system of equations. Therefore, there is no set of node voltages ($V_A, V_B, V_C, V_D$) that can satisfy Kirchhoff's Current Law at all nodes simultaneously. This means that a current $I_{AB}$ cannot be uniquely determined, or indeed, cannot exist under these conditions.