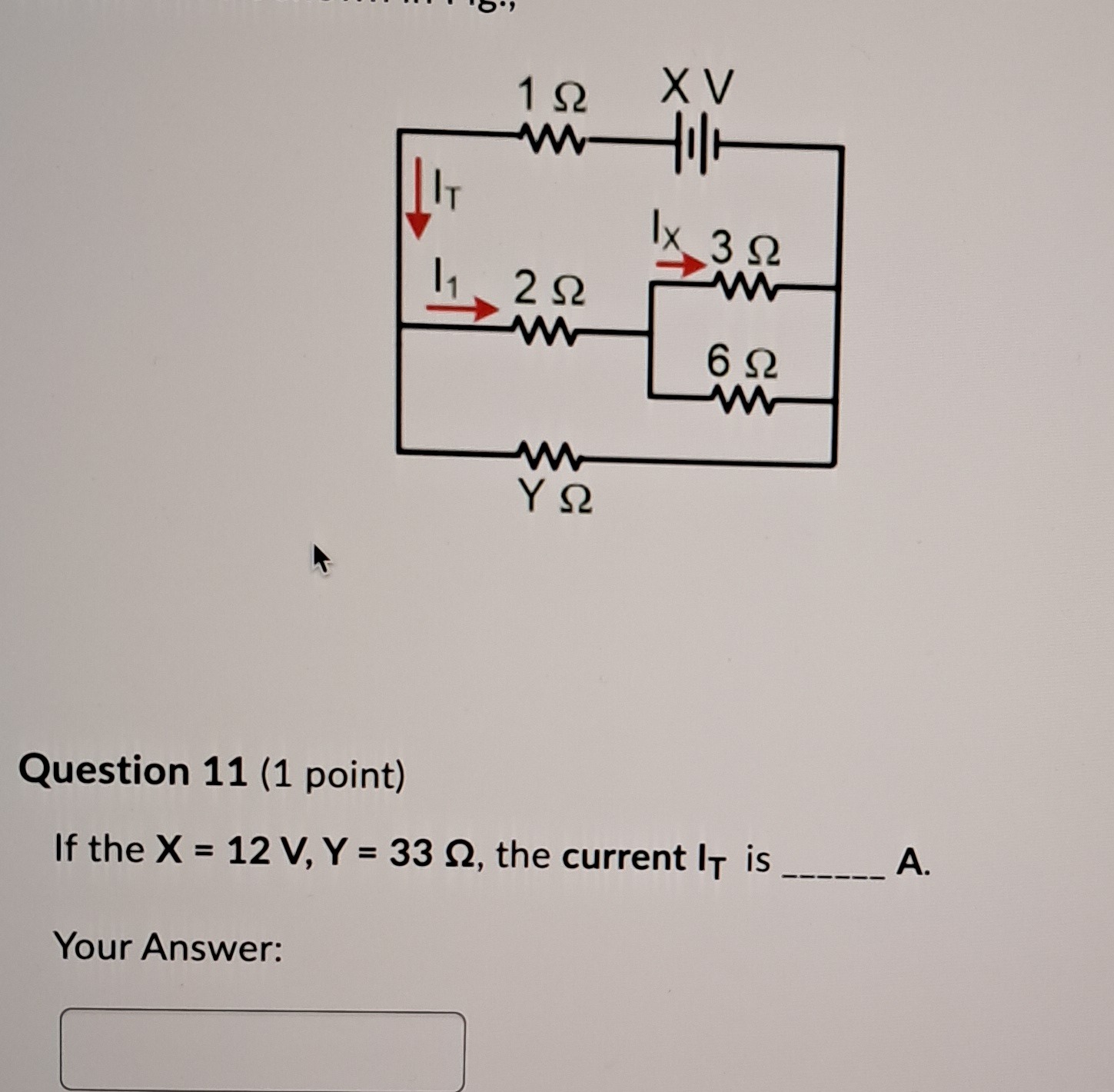
Question

If the X = 12 V, Y = 33 $\Omega$, the current IT is _______ A.

Answer 1

0.3367

Answer 2

To find the total current $I_T$ in the circuit, we need to calculate the equivalent resistance ($R_{eq}$) of the entire circuit and then apply Ohm's Law ($I_T = X / R_{eq}$).

Given values: Voltage $X = 12$ V Resistance $Y = 33 \, \Omega$

Let's break down the circuit to find the equivalent resistance:

1. Identify the series combination of the 3 $\Omega$ and 6 $\Omega$ resistors:
   The diagram shows that the current flowing through the 3 $\Omega$ resistor then flows through the 6 $\Omega$ resistor before reaching the common bottom line. Thus, they are in series.
   $R_{s1} = 3 \, \Omega + 6 \, \Omega = 9 \, \Omega$.

2. Identify the parallel combination of the 2 $\Omega$ resistor and $R_{s1}$:
   The 2 $\Omega$ resistor is connected in parallel with the series combination $R_{s1}$ (9 $\Omega$). Both branches start at the same node (after the 1 $\Omega$ resistor) and end at the common bottom line.
   $R_{p1} = \frac{2 \, \Omega \times R_{s1}}{2 \, \Omega + R_{s1}} = \frac{2 \times 9}{2 + 9} = \frac{18}{11} \, \Omega$.

3. Calculate the total equivalent resistance ($R_{eq}$):
   The 1 $\Omega$ resistor, the parallel combination $R_{p1}$ (18/11 $\Omega$), and the Y $\Omega$ resistor are all connected in series with the voltage source.
   $R_{eq} = 1 \, \Omega + R_{p1} + Y \, \Omega$.
   Substitute the given value $Y = 33 \, \Omega$:
   $R_{eq} = 1 + \frac{18}{11} + 33 = 34 + \frac{18}{11} \, \Omega$.
   To add these, find a common denominator:
   $R_{eq} = \frac{34 \times 11}{11} + \frac{18}{11} = \frac{374 + 18}{11} = \frac{392}{11} \, \Omega$.

4. Calculate the total current ($I_T$) using Ohm's Law:
   $I_T = \frac{X}{R_{eq}}$.
   Substitute the given voltage $X = 12$ V and the calculated $R_{eq}$:
   $I_T = \frac{12 \text{ V}}{\frac{392}{11} \, \Omega} = \frac{12 \times 11}{392} = \frac{132}{392}$ A.

5. Simplify the fraction:
   Divide both the numerator and the denominator by their greatest common divisor, which is 4:
   $I_T = \frac{132 \div 4}{392 \div 4} = \frac{33}{98}$ A.

The decimal value of $\frac{33}{98}$ is approximately $0.3367$.