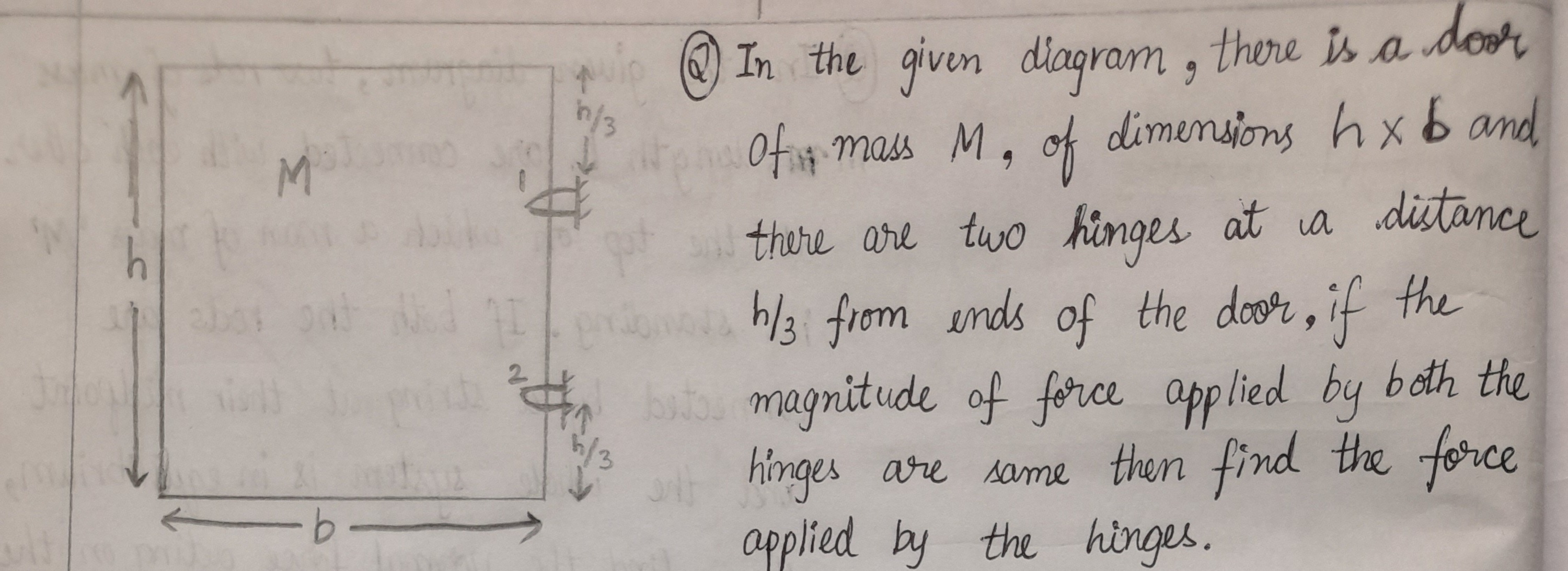
Question

In the given diagram, there is a door of mass $M$, of dimensions $h \times b$ and there are two hinges at a distance $h/3$ from ends of the door, if the magnitude of force applied by both the hinges are same then find the force applied by the hinges.

Answer 1

$\frac{Mg}{2}\sqrt{1+\frac{9b^2}{h^2}}$

Answer 2

To determine the force applied by each hinge, we analyze the door's equilibrium conditions: translational and rotational.

1. Define Variables and Setup:

• Mass of the door: $M$
• Dimensions of the door: height $h$, width $b$
• Acceleration due to gravity: $g$
• Weight of the door: $W = Mg$, acting downwards at the center of mass $(b/2, h/2)$.
• Hinge positions:
  • Top hinge (H1): at a distance $h/3$ from the top, so its vertical position is $h - h/3 = 2h/3$ from the bottom.
  • Bottom hinge (H2): at a distance $h/3$ from the bottom.
• Distance between hinges: $d = (2h/3) - (h/3) = h/3$.

Let the forces exerted by the hinges be:

• Hinge 1: $F_{H1}$ (horizontal), $F_{V1}$ (vertical)
• Hinge 2: $F_{H2}$ (horizontal), $F_{V2}$ (vertical)

2. Translational Equilibrium:

• Vertical forces: The sum of vertical forces must be zero. $F_{V1} + F_{V2} - Mg = 0$ $F_{V1} + F_{V2} = Mg \quad (1)$
• Horizontal forces: The sum of horizontal forces must be zero. The horizontal forces from the hinges must be equal and opposite to prevent the door from moving horizontally. Let's assume $F_{H1}$ acts inwards (towards the wall) and $F_{H2}$ acts outwards (away from the wall). $F_{H1} = F_{H2}$ (in magnitude). Let $F_H = F_{H1} = F_{H2}$.

3. Rotational Equilibrium: We take torques about the bottom hinge (H2) to eliminate $F_{V2}$ and $F_{H2}$ from the torque equation.

• The weight $Mg$ acts at a horizontal distance $b/2$ from the hinge line, creating a clockwise torque (tending to pull the door away from the wall). $\tau_{Mg} = Mg \times (b/2)$
• The top hinge (H1) must exert a horizontal force $F_{H1}$ to create a counter-clockwise torque to balance $\tau_{Mg}$. This means $F_{H1}$ acts inwards. The distance from H2 to H1 is $d = h/3$. $\tau_{F_{H1}} = F_{H1} \times d = F_H \times (h/3)$

For rotational equilibrium, the net torque is zero: $\tau_{F_{H1}} - \tau_{Mg} = 0$ $F_H \times (h/3) = Mg \times (b/2)$ $F_H = \frac{Mg \times b/2}{h/3} = \frac{3Mgb}{2h} \quad (2)$

4. Condition for Equal Hinge Forces: The problem states that the magnitude of force applied by both hinges is the same. Let this magnitude be $F_{hinge}$. $F_{hinge} = \sqrt{F_{H1}^2 + F_{V1}^2} = \sqrt{F_{H2}^2 + F_{V2}^2}$ Since $F_{H1} = F_{H2} = F_H$, it implies $F_{V1}^2 = F_{V2}^2$. Assuming both vertical forces act upwards (which they must to support the door's weight), we have $F_{V1} = F_{V2}$.

Substitute this into Equation (1): $F_{V1} + F_{V1} = Mg$ $2F_{V1} = Mg$ $F_{V1} = F_{V2} = \frac{Mg}{2} \quad (3)$

5. Calculate the Magnitude of Hinge Force: Now, we can find the magnitude of the force applied by each hinge using the components $F_H$ and $F_{V1}$ (or $F_{V2}$). $F_{hinge} = \sqrt{F_H^2 + F_{V1}^2}$ Substitute values from Equations (2) and (3): $F_{hinge} = \sqrt{\left(\frac{3Mgb}{2h}\right)^2 + \left(\frac{Mg}{2}\right)^2}$ $F_{hinge} = \sqrt{\frac{9M^2g^2b^2}{4h^2} + \frac{M^2g^2}{4}}$ Factor out $\frac{M^2g^2}{4}$: $F_{hinge} = \sqrt{\frac{M^2g^2}{4} \left(\frac{9b^2}{h^2} + 1\right)}$ $F_{hinge} = \frac{Mg}{2} \sqrt{\frac{9b^2}{h^2} + 1}$

The final answer is $\boxed{\frac{Mg}{2}\sqrt{1+\frac{9b^2}{h^2}}}$.

Explanation of the solution:

1. Vertical Equilibrium: The sum of upward vertical forces from hinges equals the downward weight ($Mg$). Since hinge forces are equal in magnitude, their vertical components must also be equal and upward, each supporting $Mg/2$.
2. Horizontal Equilibrium & Rotational Equilibrium: The door's weight ($Mg$) acting at its center of mass creates a torque ($Mg \times b/2$) about the hinge line, tending to pull the door away from the wall. To counteract this, the hinges must exert horizontal forces. By taking torques about one hinge (e.g., the bottom hinge), only the horizontal force of the other hinge (top hinge) contributes to balancing the weight's torque. This determines the magnitude of the horizontal force ($F_H = \frac{3Mgb}{2h}$). For horizontal translational equilibrium, the horizontal forces from the two hinges must be equal and opposite.
3. Total Hinge Force: The total force on each hinge is the vector sum of its horizontal ($F_H$) and vertical ($Mg/2$) components. Calculate the magnitude using the Pythagorean theorem: $F_{hinge} = \sqrt{F_H^2 + (Mg/2)^2}$.