Question
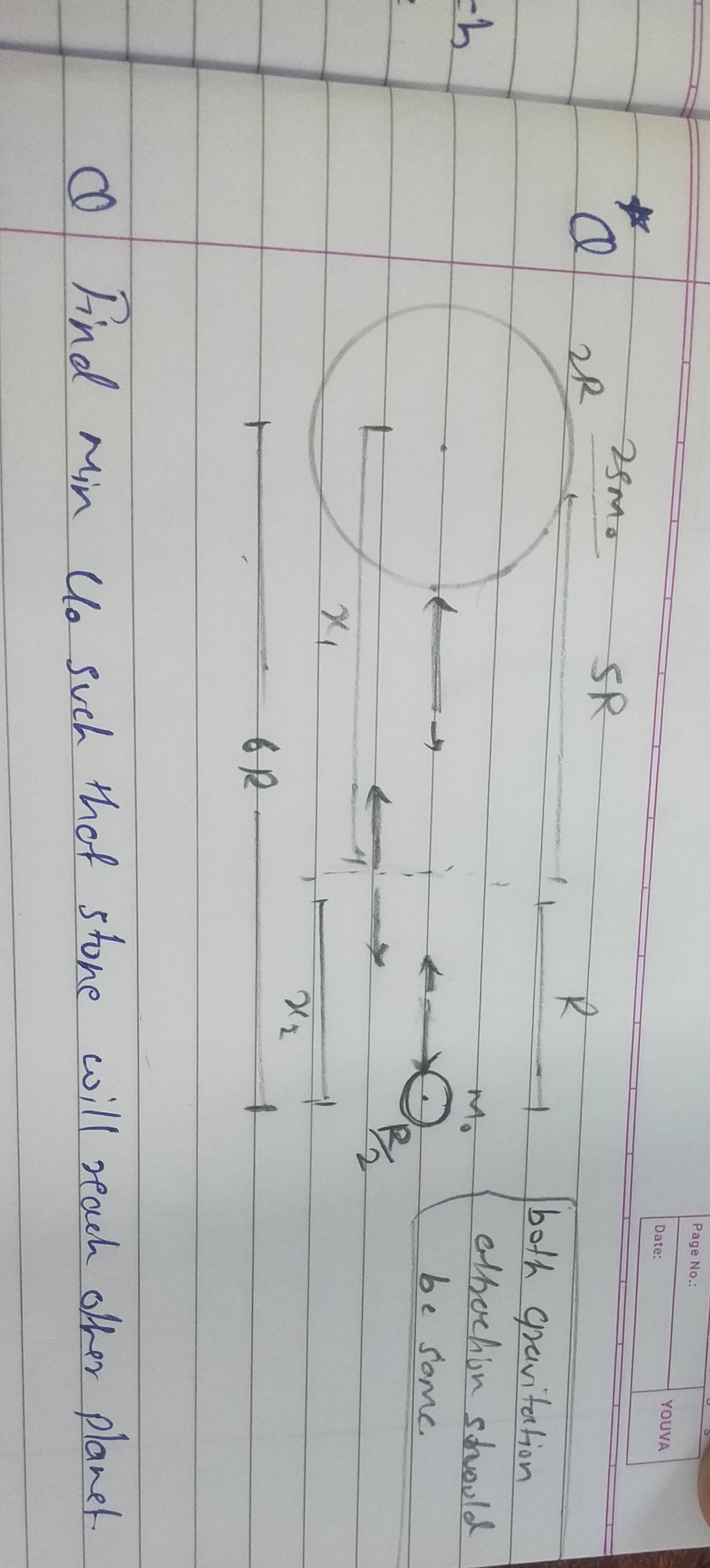
Question: Find min $U_o$ such that stone will reach other planet....
Find min Uo such that stone will reach other planet.
6R5GMm0(5+1)
Solution
The minimum initial kinetic energy (Uo) required for the stone to escape the gravitational influence of the two planets and reach infinity with zero velocity is equal to the negative of the potential energy at the point of unstable equilibrium. This point is where the net gravitational force on the stone is zero.
Let the larger planet (M1=25M) be at x=0 and the smaller planet (M2=5M) be at x=6R. The potential energy of the stone (m0) at position x is U(x)=−xGM1m0−6R−xGM2m0.
The condition for zero net force is x2GM1m0=(6R−x)2GM2m0. Substituting the masses: x225Mm0=(6R−x)25Mm0, which simplifies to 5(6R−x)2=x2. Solving for x between the planets gives the unstable equilibrium point xunstable=23(5−5)R.
The potential energy at this point is Uunstable=−6R5GMm0(5+1). Therefore, the minimum initial kinetic energy required is Uo,min=−Uunstable=6R5GMm0(5+1).
