Question

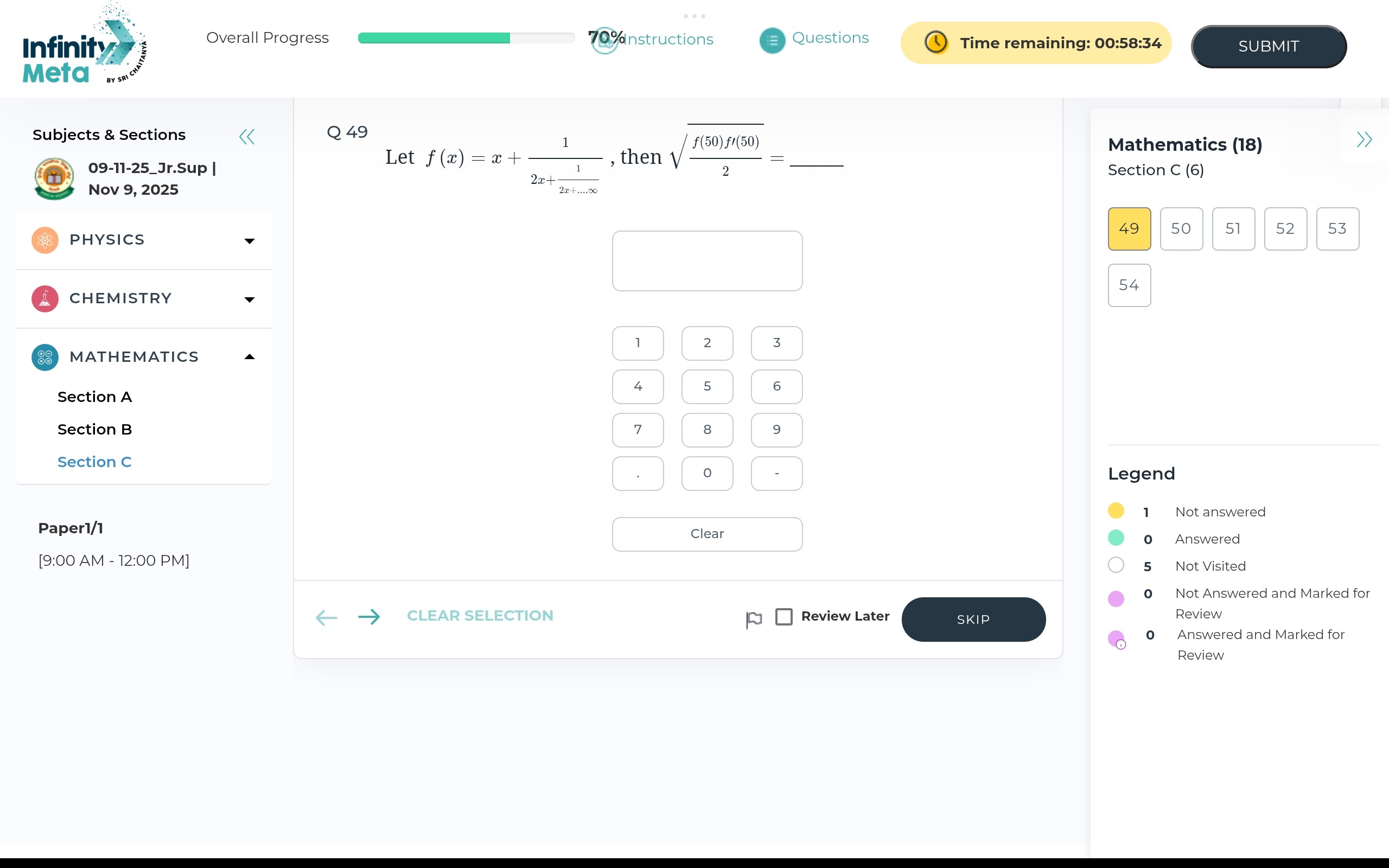
Let $f(x) = x + \frac{1}{2x+\frac{1}{2x+....\infty}}$, then $\sqrt{\frac{f(50) f'(50)}{2}} =$

• A. 1
• B. 2
• C. 3
• D. 4
• E. 5
• F. 6
• G. 7
• H. 8
• I. 9

Answer 1

Answer: (E)

5

Answer 2

Let $C = \frac{1}{2x+\frac{1}{2x+\frac{1}{2x+....\infty}}}$. Then $f(x) = x+C$. The denominator of $C$ is $D = 2x+\frac{1}{2x+\frac{1}{2x+....\infty}}$. We can see that $D = 2x+C$. Substituting this into $C = \frac{1}{D}$, we get $C = \frac{1}{2x+C}$. This leads to the quadratic equation $C^2 + 2xC - 1 = 0$. Solving for $C$, we get $C = -x \pm \sqrt{x^2+1}$. Since $x=50 > 0$, $C$ must be positive, so $C = -x + \sqrt{x^2+1}$. Then $f(x) = x+C = x + (-x + \sqrt{x^2+1}) = \sqrt{x^2+1}$. The derivative of $f(x)$ is $f'(x) = \frac{d}{dx}(\sqrt{x^2+1}) = \frac{x}{\sqrt{x^2+1}}$. Now, we evaluate $f(50)$ and $f'(50)$: $f(50) = \sqrt{50^2+1} = \sqrt{2501}$. $f'(50) = \frac{50}{\sqrt{50^2+1}} = \frac{50}{\sqrt{2501}}$. The expression to find is $\sqrt{\frac{f(50) f'(50)}{2}}$. Substituting the values: $\sqrt{\frac{\sqrt{2501} \cdot \frac{50}{\sqrt{2501}}}{2}} = \sqrt{\frac{50}{2}} = \sqrt{25} = 5$.