Solveeit Logo
Login

Question

Question: If $\alpha, \beta, \gamma$ are distinct integers, then minimum value of $\Delta$ is equal to, where ...

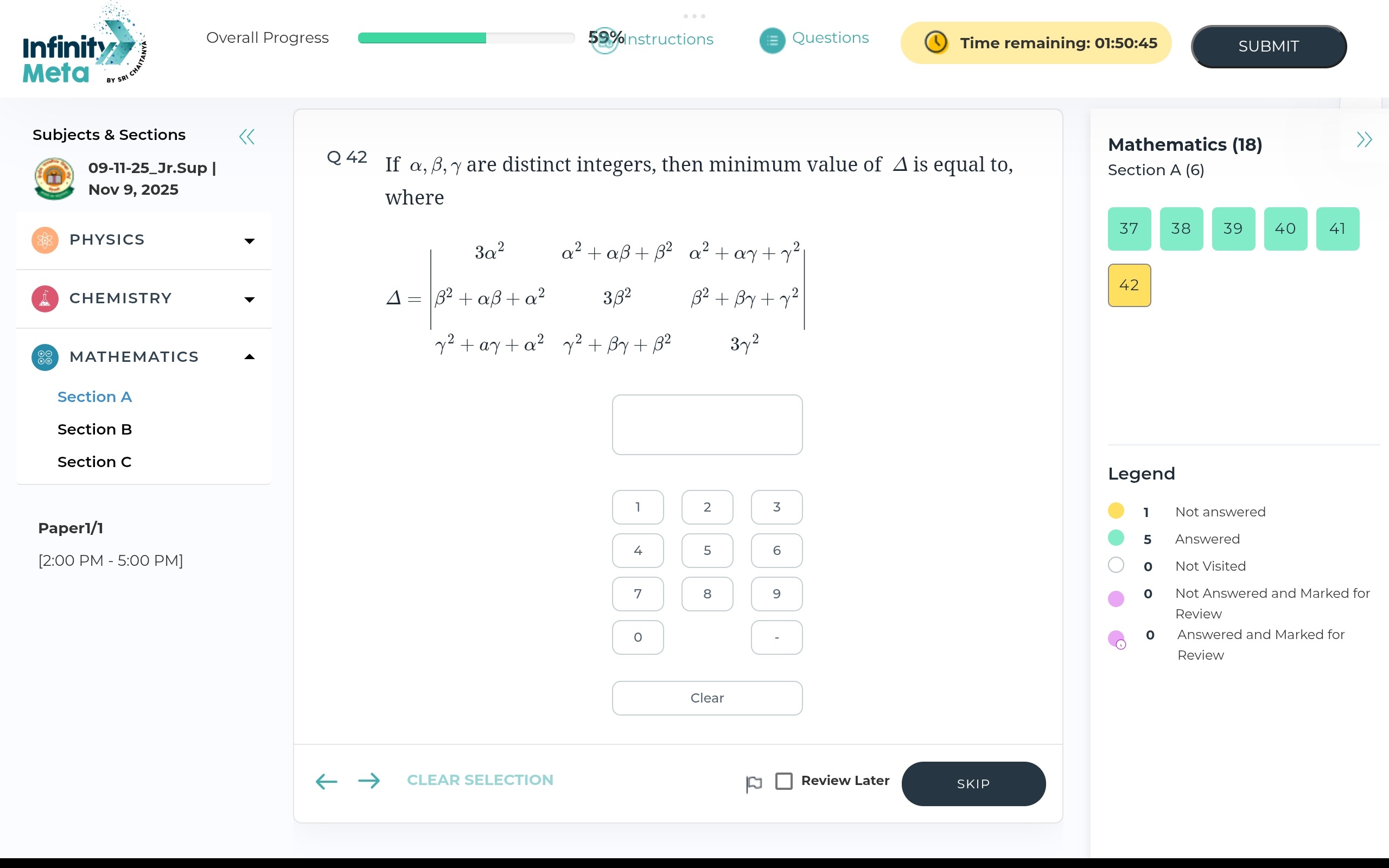
If α,β,γ\alpha, \beta, \gamma are distinct integers, then minimum value of Δ\Delta is equal to, where

Δ=∣3α2α2+αβ+β2α2+αγ+γ2β2+αβ+α23β2β2+βγ+γ2γ2+αγ+α2γ2+βγ+β23γ2∣\Delta = \begin{vmatrix} 3\alpha^2 & \alpha^2 + \alpha\beta + \beta^2 & \alpha^2 + \alpha\gamma + \gamma^2 \\ \beta^2 + \alpha\beta + \alpha^2 & 3\beta^2 & \beta^2 + \beta\gamma + \gamma^2 \\ \gamma^2 + \alpha\gamma + \alpha^2 & \gamma^2 + \beta\gamma + \beta^2 & 3\gamma^2 \end{vmatrix}

Answer

The minimum value of Δ\Delta is -4.

Explanation

Solution

Let α=0\alpha=0. Since α,β,γ\alpha, \beta, \gamma are distinct integers, β≠0\beta \neq 0 and γ≠0\gamma \neq 0, and β≠γ\beta \neq \gamma. The determinant becomes: Δ=∣0β2γ2β23β2β2+βγ+γ2γ2γ2+βγ+β23γ2∣\Delta = \begin{vmatrix} 0 & \beta^2 & \gamma^2 \\ \beta^2 & 3\beta^2 & \beta^2 + \beta\gamma + \gamma^2 \\ \gamma^2 & \gamma^2 + \beta\gamma + \beta^2 & 3\gamma^2 \end{vmatrix} Expanding along the first row: Δ=0−β2det⁡(β2β2+βγ+γ2γ23γ2)+γ2det⁡(β23β2γ2γ2+βγ+β2)\Delta = 0 - \beta^2 \det \begin{pmatrix} \beta^2 & \beta^2 + \beta\gamma + \gamma^2 \\ \gamma^2 & 3\gamma^2 \end{pmatrix} + \gamma^2 \det \begin{pmatrix} \beta^2 & 3\beta^2 \\ \gamma^2 & \gamma^2 + \beta\gamma + \beta^2 \end{pmatrix} Δ=−β2(β2⋅3γ2−γ2(β2+βγ+γ2))+γ2(β2(γ2+βγ+β2)−γ2⋅3β2)\Delta = -\beta^2 (\beta^2 \cdot 3\gamma^2 - \gamma^2(\beta^2 + \beta\gamma + \gamma^2)) + \gamma^2 (\beta^2(\gamma^2 + \beta\gamma + \beta^2) - \gamma^2 \cdot 3\beta^2) Δ=−β2(3β2γ2−β2γ2−βγ3−γ4)+γ2(β2γ2+β3γ+β4−3β2γ2)\Delta = -\beta^2 (3\beta^2\gamma^2 - \beta^2\gamma^2 - \beta\gamma^3 - \gamma^4) + \gamma^2 (\beta^2\gamma^2 + \beta^3\gamma + \beta^4 - 3\beta^2\gamma^2) Δ=−β2(2β2γ2−βγ3−γ4)+γ2(β4+β3γ−2β2γ2)\Delta = -\beta^2 (2\beta^2\gamma^2 - \beta\gamma^3 - \gamma^4) + \gamma^2 (\beta^4 + \beta^3\gamma - 2\beta^2\gamma^2) Δ=−2β4γ2+β3γ3+β2γ4+β4γ2+β3γ3−2β2γ4\Delta = -2\beta^4\gamma^2 + \beta^3\gamma^3 + \beta^2\gamma^4 + \beta^4\gamma^2 + \beta^3\gamma^3 - 2\beta^2\gamma^4 Δ=−β4γ2+2β3γ3−β2γ4=−β2γ2(β2−2βγ+γ2)=−β2γ2(β−γ)2\Delta = -\beta^4\gamma^2 + 2\beta^3\gamma^3 - \beta^2\gamma^4 = -\beta^2\gamma^2 (\beta^2 - 2\beta\gamma + \gamma^2) = -\beta^2\gamma^2 (\beta - \gamma)^2 Since β\beta and γ\gamma are distinct non-zero integers, β2>0\beta^2 > 0, γ2>0\gamma^2 > 0, and (β−γ)2>0(\beta - \gamma)^2 > 0. Thus, Δ=−β2γ2(β−γ)2\Delta = -\beta^2\gamma^2 (\beta - \gamma)^2 is always negative. To minimize Δ\Delta, we need to maximize β2γ2(β−γ)2\beta^2\gamma^2 (\beta - \gamma)^2. Let's test some small distinct integer values for β\beta and γ\gamma (with α=0\alpha=0):

  • If β=1,γ=2\beta=1, \gamma=2: Δ=−(12)(22)(1−2)2=−(1)(4)(−1)2=−4\Delta = -(1^2)(2^2)(1-2)^2 = -(1)(4)(-1)^2 = -4.
  • If β=2,γ=1\beta=2, \gamma=1: Δ=−(22)(12)(2−1)2=−(4)(1)(1)2=−4\Delta = -(2^2)(1^2)(2-1)^2 = -(4)(1)(1)^2 = -4.
  • If β=1,γ=−1\beta=1, \gamma=-1: Δ=−(12)(−1)2(1−(−1))2=−(1)(1)(2)2=−4\Delta = -(1^2)(-1)^2(1-(-1))^2 = -(1)(1)(2)^2 = -4.
  • If β=−1,γ=1\beta=-1, \gamma=1: Δ=−(−1)2(12)(−1−1)2=−(1)(1)(−2)2=−4\Delta = -(-1)^2(1^2)(-1-1)^2 = -(1)(1)(-2)^2 = -4.
  • If β=1,γ=−2\beta=1, \gamma=-2: Δ=−(12)(−2)2(1−(−2))2=−(1)(4)(3)2=−36\Delta = -(1^2)(-2)^2(1-(-2))^2 = -(1)(4)(3)^2 = -36.
  • If β=2,γ=−1\beta=2, \gamma=-1: Δ=−(22)(−1)2(2−(−1))2=−(4)(1)(3)2=−36\Delta = -(2^2)(-1)^2(2-(-1))^2 = -(4)(1)(3)^2 = -36.

The minimum value observed is -4. It is known that the minimum value of this determinant for distinct integers is -4, achieved when the integers are 0, 1, and -1 in any permutation, or 0, 1, 2, etc. yielding -4.