Question
Question: If $x, y, z$ are non-zero real numbers and $\begin{vmatrix} 1+x & 1 & 1 \\ 1+y & 1+2y & 1 \\ 1+z & 1...
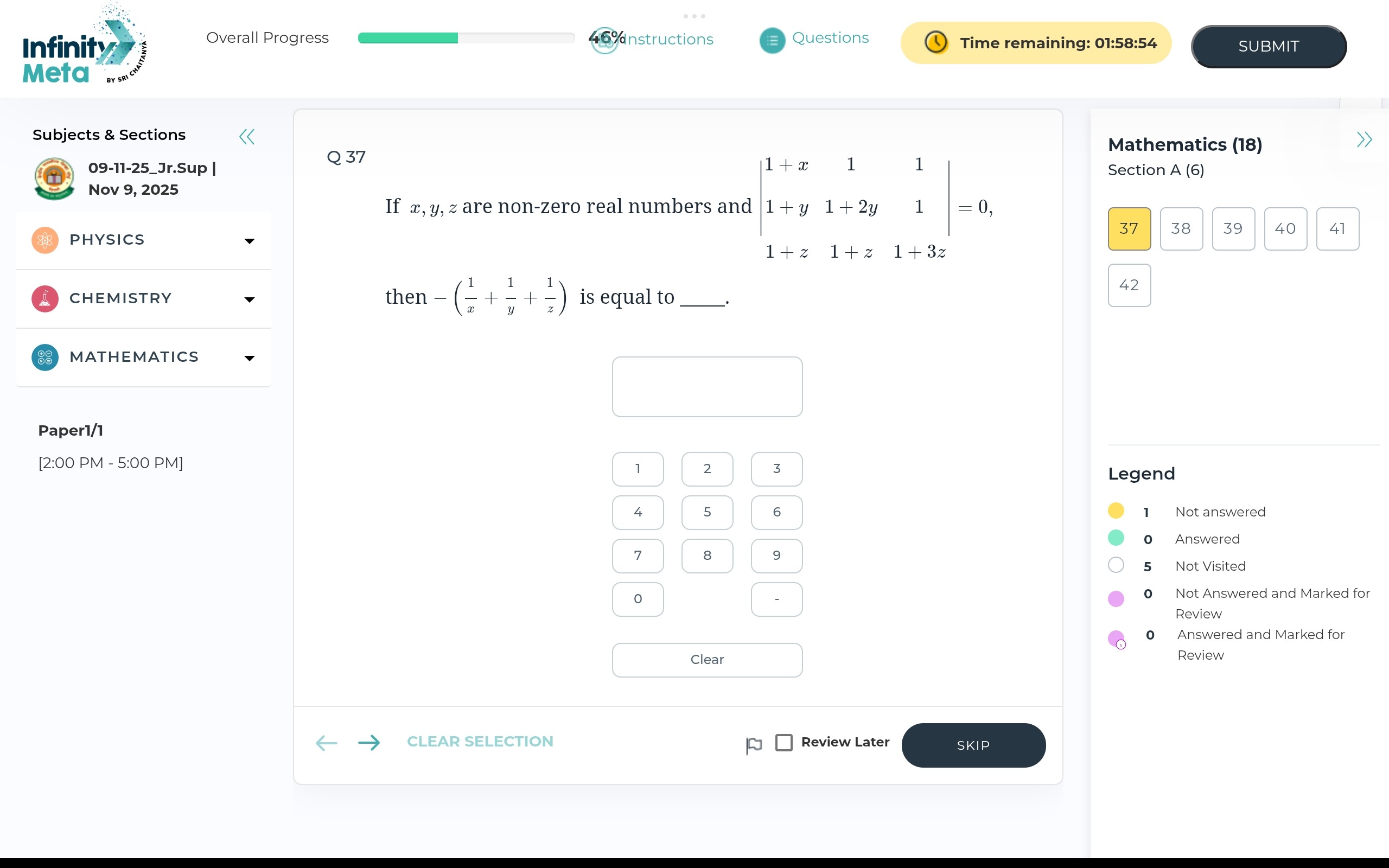
If x,y,z are non-zero real numbers and 1+x1+y1+z11+2y1+z111+3z=0, then −(x1+y1+z1) is equal to ____.
Answer
3
Explanation
Solution
Apply column operations C1→C1−C2 and C2→C2−C3 to the determinant. 1+x1+y1+z11+2y1+z111+3z=x−y002y−2z111+3z Expand along the first row: x2y−2z11+3z−0+1−y02y−2z=0 x(2y(1+3z)−(1)(−2z))+(−y)(−2z)−(2y)(0)=0 x(2y+6yz+2z)+2yz=0 2xy+6xyz+2xz+2yz=0 Divide by 2xyz (since x,y,z=0): z1+3+y1+x1=0 x1+y1+z1=−3 Therefore, −(x1+y1+z1)=−(−3)=3.
