Question

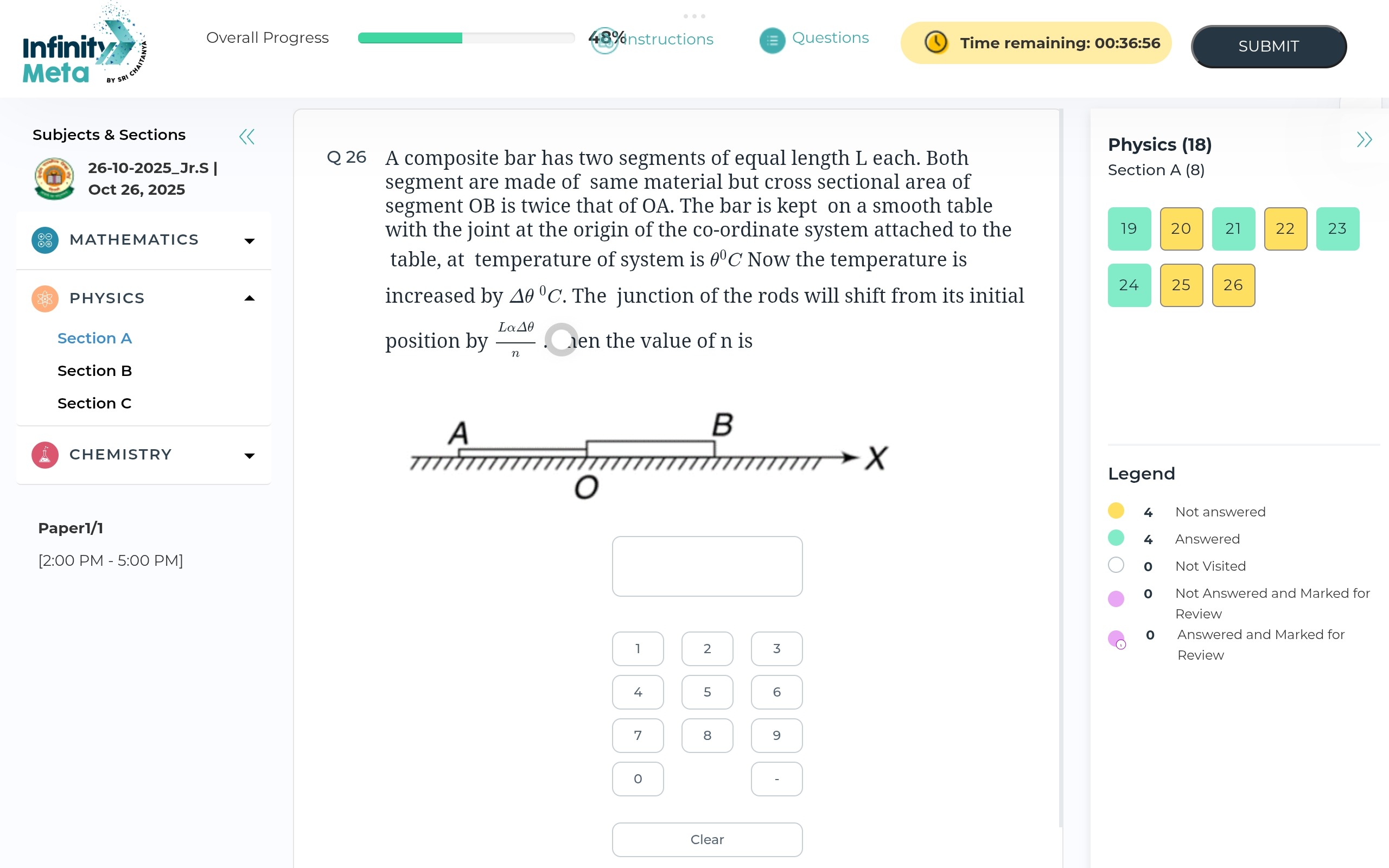
A composite bar has two segments of equal length L each. Both segment are made of same material but cross sectional area of segment OB is twice that of OA. The bar is kept on a smooth table with the joint at the origin of the co-ordinate system attached to the table, at temperature of system is $\theta^{\circ}C$ Now the temperature is increased by $\Delta\theta^{\circ}C$. The junction of the rods will shift from its initial position by $\frac{L\alpha\Delta\theta}{n}$. Then the value of n is

• A. 3
• B. -3
• C. 1/3
• D. -1/3

Answer 1

Answer: (D)

The value of n is -1/3.

Answer 2

Let the cross-sectional area of segment OA be $A$ and that of OB be $2A$. Let the initial position of the joint be at the origin $O$. Let segment OA be from $x=-L$ to $x=0$ and segment OB be from $x=0$ to $x=L$. Let the final position of the joint be $x_j$.

The final length of segment OA is $L'_{OA} = x_j - (-L) = x_j + L$. The strain in OA is $\epsilon_{OA} = \frac{L'_{OA} - L}{L} = \frac{x_j}{L}$. The final length of segment OB is $L'_{OB} = L - x_j$. The strain in OB is $\epsilon_{OB} = \frac{L'_{OB} - L}{L} = \frac{-x_j}{L}$.

The total strain in each segment is the sum of thermal strain and mechanical strain: $\epsilon = \alpha \Delta\theta + \sigma/E$. So, $\frac{x_j}{L} = \alpha \Delta\theta + \frac{\sigma_{OA}}{E}$ and $\frac{-x_j}{L} = \alpha \Delta\theta + \frac{\sigma_{OB}}{E}$.

Due to force equilibrium at the joint, the force exerted by OA on OB is equal and opposite to the force exerted by OB on OA. Thus, $\sigma_{OA} A = -\sigma_{OB} (2A)$, which gives $\sigma_{OA} = -2\sigma_{OB}$.

Substituting $\sigma_{OA} = -2\sigma_{OB}$ into the strain equations and solving for $x_j$: $\frac{\sigma_{OA}}{E} = \frac{x_j}{L} - \alpha \Delta\theta$ $\frac{\sigma_{OB}}{E} = \frac{-x_j}{L} - \alpha \Delta\theta$

Substituting these into $\sigma_{OA} = -2\sigma_{OB}$: $E(\frac{x_j}{L} - \alpha \Delta\theta) = -2E(\frac{-x_j}{L} - \alpha \Delta\theta)$ $\frac{x_j}{L} - \alpha \Delta\theta = \frac{2x_j}{L} + 2\alpha \Delta\theta$ $-\frac{x_j}{L} = 3\alpha \Delta\theta \implies x_j = -3L\alpha\Delta\theta$.

The shift in position is $x_j$. The question states the shift is $\frac{L\alpha\Delta\theta}{n}$. Therefore, $\frac{L\alpha\Delta\theta}{n} = -3L\alpha\Delta\theta$. This implies $\frac{1}{n} = -3$, so $n = -\frac{1}{3}$.