Question

Three steel rods of equal length form an equilateral triangle ABC. Taking midpoint of BC as origin, the increase in y-coordinate of centre of mass per unit change in temperature is n × 10-6m. Then n = _______(Assuming the length of each rod is 2m and $\alpha_s$ = 4√3 × 10-6/°C)

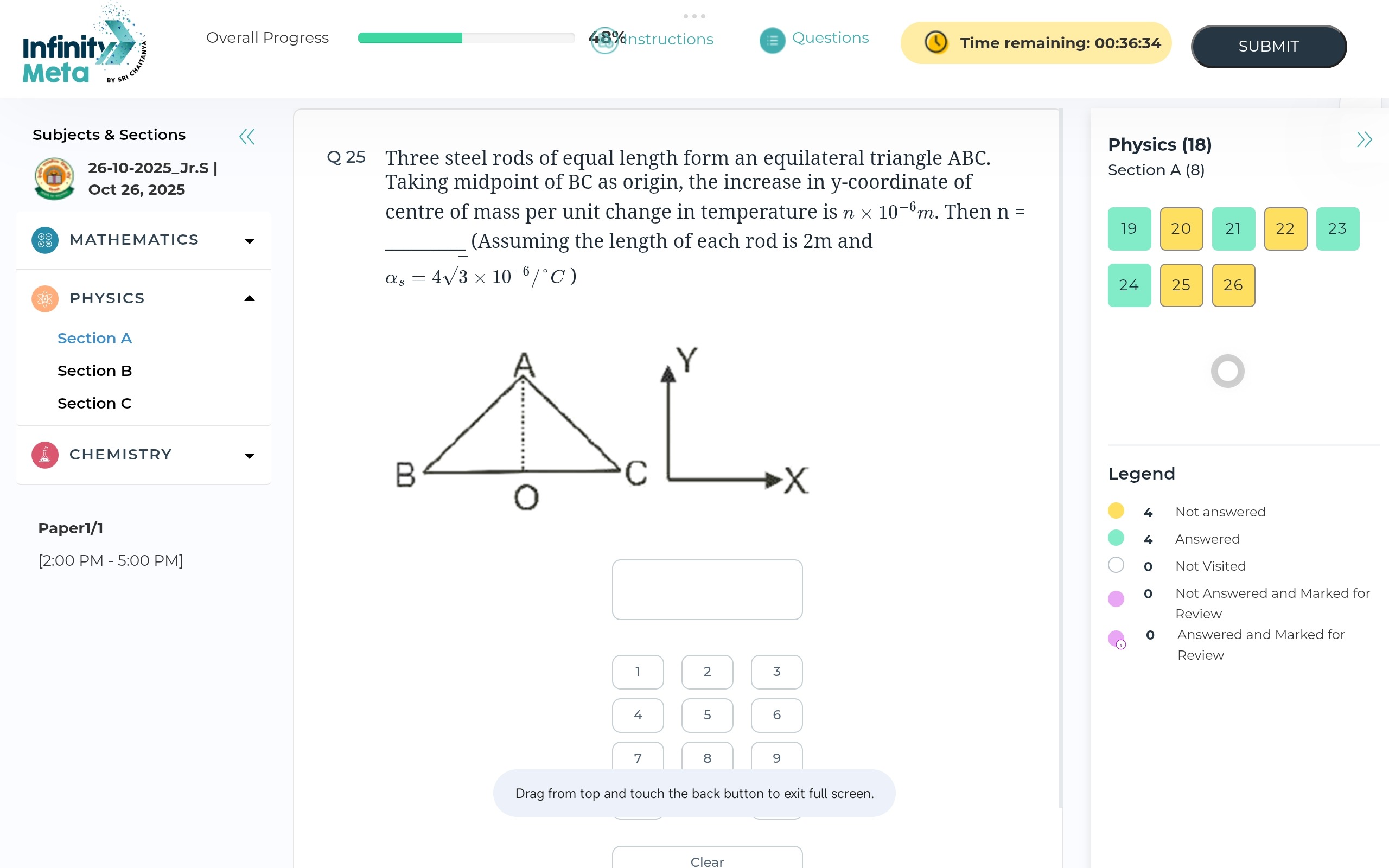
Answer 1

4

Answer 2

The y-coordinate of the center of mass of the equilateral triangle is $Y_{CM} = \frac{\sqrt{3}}{3}(1 + \alpha_s \Delta T)$. The rate of change of $Y_{CM}$ with respect to temperature is $\frac{dY_{CM}}{d(\Delta T)} = \frac{\sqrt{3}}{3} \alpha_s$. Substituting $\alpha_s = 4\sqrt{3} \times 10^{-6} /^\circ C$, we get $\frac{dY_{CM}}{d(\Delta T)} = \frac{\sqrt{3}}{3} \times (4\sqrt{3} \times 10^{-6}) = 4 \times 10^{-6}$ m/°C. Comparing this with $n \times 10^{-6}$ m/°C, we find $n = 4$.