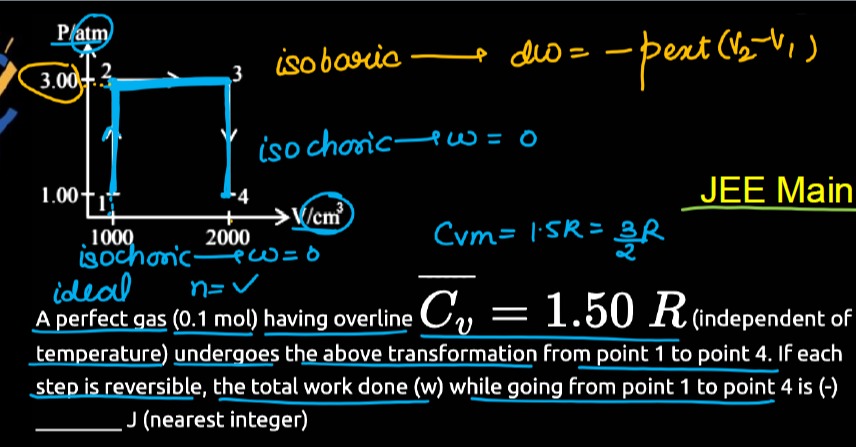
Question: P/atm 3. 00 isobaric $\longrightarrow$ dw= $-P_{ext}(V_{2}-V_{1})$ 1. 00 1 2. 000 V/cm³ isocho...

Question

P/atm

00 isobaric $\longrightarrow$ dw= $-P_{ext}(V_{2}-V_{1})$
00 1
000 V/cm³ isochoric $\longrightarrow$ w = 0

isochoric $\longrightarrow$ w = 0

JEE Main

$C_{vm}$ = 1.5R = $\frac{3}{2}R$

$\overline{C_{v}}$ = 1.50 R(independent of temperature) undergoes the above transformation from point 1 to point 4. If each step is reversible, the total work done (w) while going from point 1 to point 4 is (-) J (nearest integer)

Answer 1

Solution

The transformation consists of three steps: 1 → 2 (isochoric), 2 → 3 (isobaric), and 3 → 4 (isochoric).

Isochoric processes (1 → 2 and 3 → 4): Work done $w = 0$ as there is no change in volume ( $\Delta V = 0$ ).
Isobaric process (2 → 3):
- Pressure $P = 3.00$ atm.
- Volume change: $V_2 = 1000$ cm³ = 1 L, $V_3 = 2000$ cm³ = 2 L.
- Work done $w_{2\to3} = P \Delta V = 3.00 \, \text{atm} \times (2\, \text{L} - 1\, \text{L}) = 3.00 \, \text{L·atm}$ .
Conversion to Joules:
- Using the conversion factor $1 \, \text{L·atm} = 101.325 \, \text{J}$ .
- $w_{2\to3} = 3.00 \times 101.325 \, \text{J} \approx 303.975 \, \text{J}$ .

The question asks for the total work done (w) and specifies the answer format as (-)_____ J, indicating work done on the system. The work done by the system during expansion (2 → 3) is positive. Therefore, the work done on the system is negative.

Total work done $w = w_{1\to2} + w_{2\to3} + w_{3\to4} = 0 + (-303.975 \, \text{J}) + 0 \approx -304 \, \text{J}$ . The value to fill in the blank is 304.