Question

$\newline$ $\newline$ $P_1$ $\newline$ $P_A$ $\newline$ $P_B$ $\newline$ $P_C$ $\newline$ $V_1$ $\newline$ $V_2$ $\newline$ V$\rightarrow$ till a fix $V_2$ volume $\newline$ $P_1,V_1,T_1$ more $\Gamma$

Answer 1

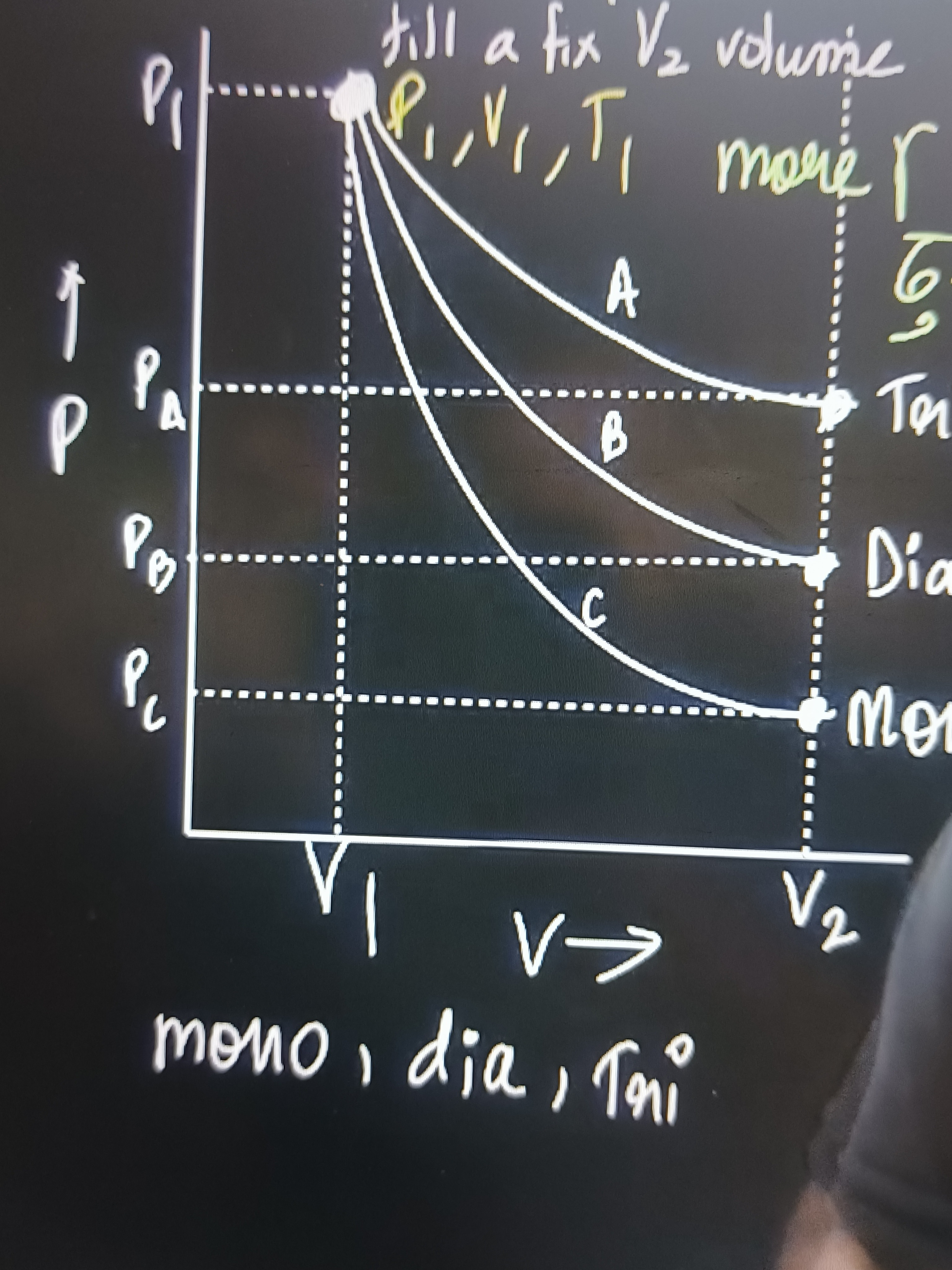
A corresponds to Triatomic, B to Diatomic, C to Monoatomic

Answer 2

The problem presents a P-V diagram showing three adiabatic expansion curves (A, B, C) starting from a common initial state $(P_1, V_1)$ and expanding to a common final volume $V_2$. The final pressures are $P_A, P_B, P_C$ respectively, with $P_A > P_B > P_C$. The curves are labeled "Tri", "Dia", and "Mono" at their respective final points. We need to understand the physical principle behind this representation.

For an adiabatic process, the relationship between pressure and volume is given by: $PV^\gamma = \text{constant}$ where $\gamma = \frac{C_p}{C_v}$ is the adiabatic index (or Poisson's ratio).

Let's consider the expansion from an initial state $(P_1, V_1)$ to a final state $(P_f, V_2)$. $P_1 V_1^\gamma = P_f V_2^\gamma$ The final pressure $P_f$ can be expressed as: $P_f = P_1 \left(\frac{V_1}{V_2}\right)^\gamma$

In this problem, $V_2 > V_1$, so the ratio $\frac{V_1}{V_2}$ is less than 1. Let $k = \frac{V_1}{V_2}$, where $0 < k < 1$. So, $P_f = P_1 k^\gamma$.

Now, let's recall the values of $\gamma$ for different types of ideal gases (assuming moderate temperatures where vibrational modes are not excited):

1. Monoatomic gas: Degrees of freedom ($f$) = 3 (translational). The adiabatic index is $\gamma_{mono} = 1 + \frac{2}{f} = 1 + \frac{2}{3} = \frac{5}{3} \approx 1.67$.

2. Diatomic gas: Degrees of freedom ($f$) = 5 (3 translational + 2 rotational). The adiabatic index is $\gamma_{dia} = 1 + \frac{2}{f} = 1 + \frac{2}{5} = \frac{7}{5} = 1.4$.

3. Triatomic gas (non-linear): Degrees of freedom ($f$) = 6 (3 translational + 3 rotational). The adiabatic index is $\gamma_{tri} = 1 + \frac{2}{f} = 1 + \frac{2}{6} = \frac{4}{3} \approx 1.33$. (Note: If the triatomic molecule is linear, like CO$_2$, its degrees of freedom for rotation are 2, making $f=5$ and $\gamma=1.4$. However, in such comparative problems, "triatomic" usually refers to the general non-linear case unless specified, implying a distinct $\gamma$ from diatomic).

Comparing the $\gamma$ values, we have the order: $\gamma_{mono} (\approx 1.67) > \gamma_{dia} (1.4) > \gamma_{tri} (\approx 1.33)$

From the graph, for the same expansion from $V_1$ to $V_2$, the final pressures are observed to be: $P_A > P_B > P_C$.

Now, let's relate the final pressure $P_f$ to $\gamma$ using $P_f = P_1 k^\gamma$ where $0 < k < 1$. Since $k < 1$, as the exponent $\gamma$ increases, the value of $k^\gamma$ decreases. Consequently, $P_f$ decreases as $\gamma$ increases. This means:

• The gas with the smallest $\gamma$ will have the highest final pressure ($P_f$).
• The gas with the largest $\gamma$ will have the lowest final pressure ($P_f$).

Applying this to the observed pressures from the graph:

• Curve A results in the highest final pressure ($P_A$). This implies that the gas undergoing process A has the smallest $\gamma$. Therefore, Curve A corresponds to a Triatomic gas ($\gamma_{tri} \approx 1.33$).
• Curve B results in an intermediate final pressure ($P_B$). This implies that the gas undergoing process B has an intermediate $\gamma$. Therefore, Curve B corresponds to a Diatomic gas ($\gamma_{dia} = 1.4$).
• Curve C results in the lowest final pressure ($P_C$). This implies that the gas undergoing process C has the largest $\gamma$. Therefore, Curve C corresponds to a Monoatomic gas ($\gamma_{mono} \approx 1.67$).

This analysis is consistent with the labels provided in the diagram:

• Curve A is labeled "Tri".
• Curve B is labeled "Dia".
• Curve C is labeled "Mono".

The slope of an adiabatic curve on a P-V diagram is given by $\frac{dP}{dV} = -\gamma \frac{P}{V}$. For a given initial point $(P_1, V_1)$, a larger $\gamma$ implies a steeper negative slope. Visually, curve C is the steepest, followed by B, and then A is the least steep, which also confirms $\gamma_C > \gamma_B > \gamma_A$.