Question

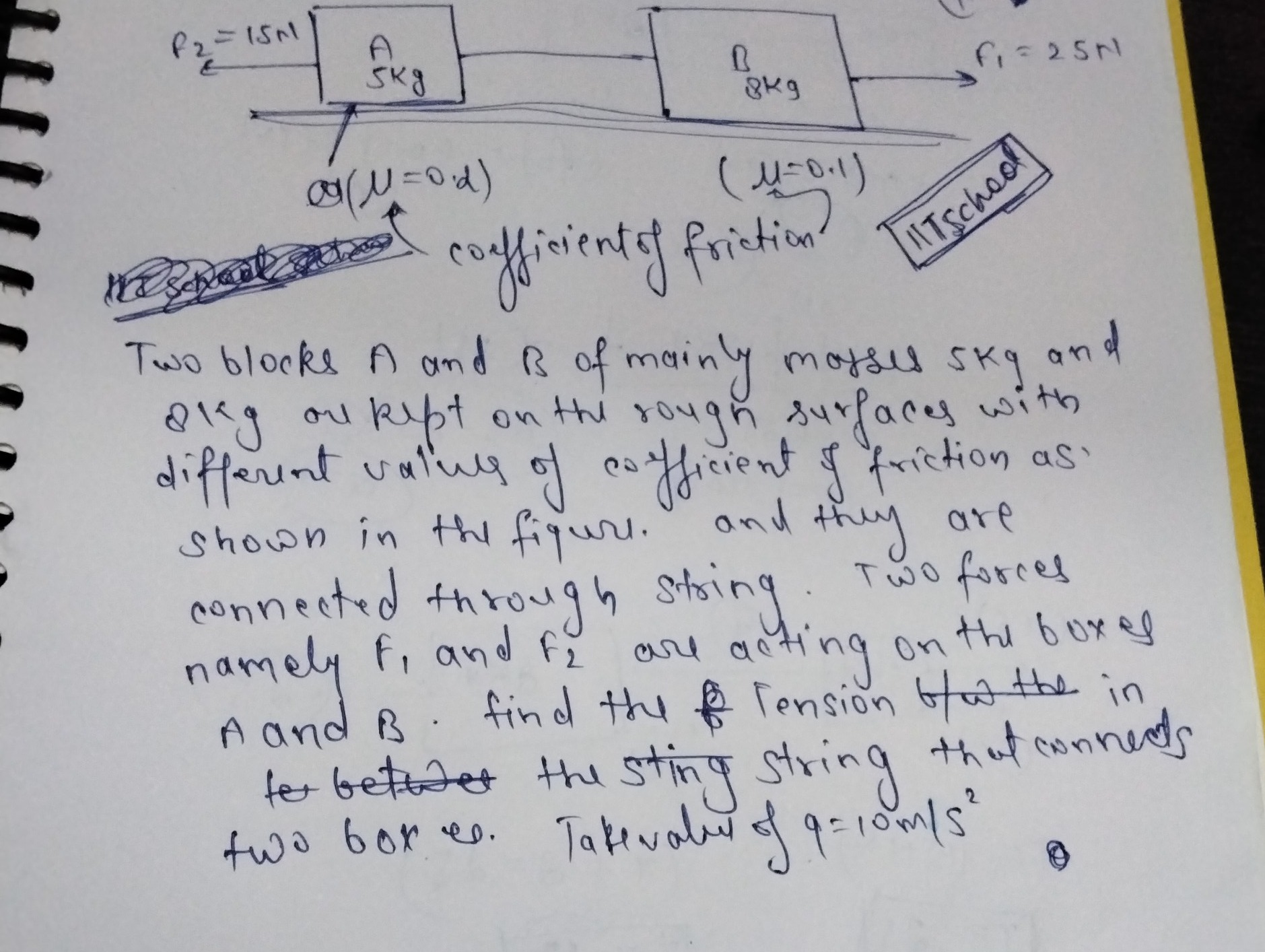
Two blocks A and B of mainly masses 5kg and 8kg ou kept on the rough surfaces with different values of coefficient of friction as shown in the figure. and they are connected through String. Two forces namely F₁ and F₂ are acting on the boxes A and B. find the & Tension of the in for betwer the sting string that connects two box es. Take value of g=10m/s²

Answer 1

20N

Answer 2

The system consists of two blocks A and B connected by a string, placed on a rough horizontal surface. External forces $P_2 = 15$ N and $F_1 = 25$ N are applied to blocks A and B respectively. The masses are $m_A = 5$ kg and $m_B = 8$ kg. The coefficients of kinetic friction are $\mu_A = 0.2$ and $\mu_B = 0.1$. We take $g = 10$ m/s².

First, let's calculate the maximum static friction for each block. The normal force on each block is equal to its weight since the surface is horizontal. $N_A = m_A g = 5 \times 10 = 50$ N. The maximum static friction for block A is $f_{sA,max} = \mu_A N_A = 0.2 \times 50 = 10$ N. $N_B = m_B g = 8 \times 10 = 80$ N. The maximum static friction for block B is $f_{sB,max} = \mu_B N_B = 0.1 \times 80 = 8$ N.

Let's check if the system moves. Consider the net external force on the system in the horizontal direction. The force $F_1$ acts to the right, and the force $P_2$ acts to the left. The net external force is $F_{net} = F_1 - P_2 = 25 - 15 = 10$ N to the right. The maximum possible static friction opposing motion is the sum of the maximum static frictions for each block: $f_{s,max} = f_{sA,max} + f_{sB,max} = 10 + 8 = 18$ N. Since the net external force (10 N) is less than the maximum total static friction (18 N), the system will remain at rest. The acceleration of the system is $a = 0$.

Since the system is at rest, the net force on each block is zero. Let $T$ be the tension in the string.

Let's assume the tension is 20 N. For A: $15 - 20 + f_A = 0 \implies f_A = 5$. $|f_A| = 5 \le 10$. Valid. For B: $25 - 20 + f_B = 0 \implies f_B = -5$. $|f_B| = 5 \le 8$. Valid. With $T=20$, $f_A=5$ (right) and $f_B=5$ (left). Check equilibrium of A: $15 - 20 + 5 = 0$. Valid. Check equilibrium of B: $25 - 20 - 5 = 0$. Valid.

The tension in the string is 20 N.