Question

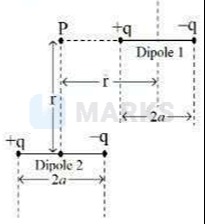
p

+q -q

Dipole 1

r

2a

-q +q

Dipole 2

2a

• A. The potential energy is $U = \frac{1}{4\pi\epsilon_0} \frac{p^2}{4\sqrt{2} r^3}$
• B. The potential energy is $U = - \frac{1}{4\pi\epsilon_0} \frac{p^2}{4\sqrt{2} r^3}$
• C. The potential energy is $U = - \frac{1}{4\pi\epsilon_0} \frac{3p^2}{4\sqrt{2} r^3}$
• D. The potential energy is $U = \frac{1}{4\pi\epsilon_0} \frac{3p^2}{4\sqrt{2} r^3}$

Answer 1

Answer: (B)

• \frac{1}{4\pi\epsilon_0} \frac{p^2}{4\sqrt{2} r^3}

Answer 2

The interaction potential energy $U$ between two dipoles $\vec{p}_1$ and $\vec{p}_2$ separated by a vector $\vec{R}$ is given by: $U = \frac{1}{4\pi\epsilon_0} \left( \frac{\vec{p}_1 \cdot \vec{p}_2}{R^3} - 3 \frac{(\vec{p}_1 \cdot \hat{R})(\vec{p}_2 \cdot \hat{R})}{R^3} \right)$ Assuming Dipole 2 is at the origin $(0,0)$ with its dipole moment along the x-axis, $\vec{p}_2 = p \hat{i}$. The diagram suggests that Dipole 1 is positioned such that its center is at $(r,r)$. If we assume Dipole 1 is also oriented along the x-axis, parallel to Dipole 2, then $\vec{p}_1 = p \hat{i}$. The vector connecting the centers of the dipoles is $\vec{R} = r\hat{i} + r\hat{j}$. The magnitude of this vector is $R = |\vec{R}| = \sqrt{r^2 + r^2} = r\sqrt{2}$. The unit vector in the direction of $\vec{R}$ is $\hat{R} = \frac{\vec{R}}{R} = \frac{r\hat{i} + r\hat{j}}{r\sqrt{2}} = \frac{1}{\sqrt{2}}(\hat{i} + \hat{j})$.

Now, we compute the dot products: $\vec{p}_1 \cdot \vec{p}_2 = (p \hat{i}) \cdot (p \hat{i}) = p^2$ $\vec{p}_1 \cdot \hat{R} = (p \hat{i}) \cdot \left(\frac{1}{\sqrt{2}}(\hat{i} + \hat{j})\right) = \frac{p}{\sqrt{2}}$ $\vec{p}_2 \cdot \hat{R} = (p \hat{i}) \cdot \left(\frac{1}{\sqrt{2}}(\hat{i} + \hat{j})\right) = \frac{p}{\sqrt{2}}$

Substitute these into the potential energy formula: $U = \frac{1}{4\pi\epsilon_0} \left( \frac{p^2}{(r\sqrt{2})^3} - 3 \frac{\left(\frac{p}{\sqrt{2}}\right)\left(\frac{p}{\sqrt{2}}\right)}{(r\sqrt{2})^3} \right)$ $U = \frac{1}{4\pi\epsilon_0} \left( \frac{p^2}{r^3 (2\sqrt{2})} - 3 \frac{\frac{p^2}{2}}{r^3 (2\sqrt{2})} \right)$ $U = \frac{1}{4\pi\epsilon_0} \frac{p^2}{r^3 (2\sqrt{2})} \left( 1 - \frac{3}{2} \right)$ $U = \frac{1}{4\pi\epsilon_0} \frac{p^2}{r^3 (2\sqrt{2})} \left( -\frac{1}{2} \right)$ $U = - \frac{1}{4\pi\epsilon_0} \frac{p^2}{4\sqrt{2} r^3}$ This result assumes that both dipoles are aligned parallel to each other and pointing in the same direction. The diagram's charge distribution (+q on left, -q on right) for both dipoles suggests a horizontal orientation, and the label 'p' without an arrow on Dipole 1 could imply its moment is also horizontal. The upward arrow next to 'p' on Dipole 1 in the diagram is ambiguous and is disregarded in favor of the charge distribution for determining dipole orientation. The magnitude $p$ is given by $q \times 2a$.