Question

Work done by polytropic process formula and area of graph are coming different. why?

Answer 1

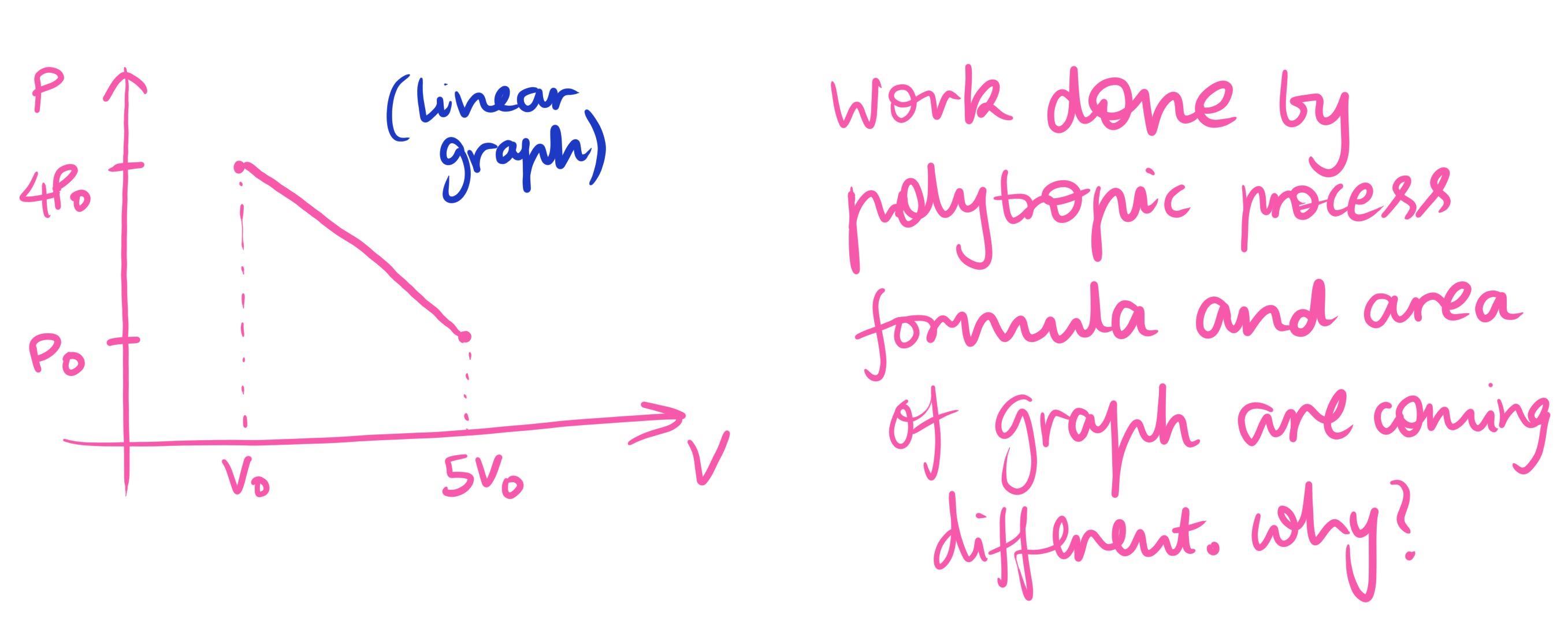
The discrepancy arises because the given process is a linear relationship between pressure and volume, while the polytropic process formula is derived for processes that follow the relationship $PV^n = \text{constant}$. A linear process is not generally equivalent to $PV^n = \text{constant}$ for a single value of $n$. Therefore, the polytropic formula is not applicable to this linear process, leading to a different result than the actual work done calculated from the area under the graph.

Answer 2

The given process is a linear relationship between pressure (P) and volume (V). The work done by the gas is represented by the area under the P-V graph. The formula for work done in a polytropic process, $W = \frac{P_2V_2 - P_1V_1}{1-n}$, is derived under the assumption that the process follows the relation $PV^n = \text{constant}$. A linear relationship between P and V ($P = mV + c$) is generally not equivalent to $PV^n = \text{constant}$ for any single value of $n$. Since the given linear process is not a polytropic process of the form $PV^n = \text{constant}$, applying the polytropic formula to it yields a result different from the actual work done calculated from the area under the graph.