Question

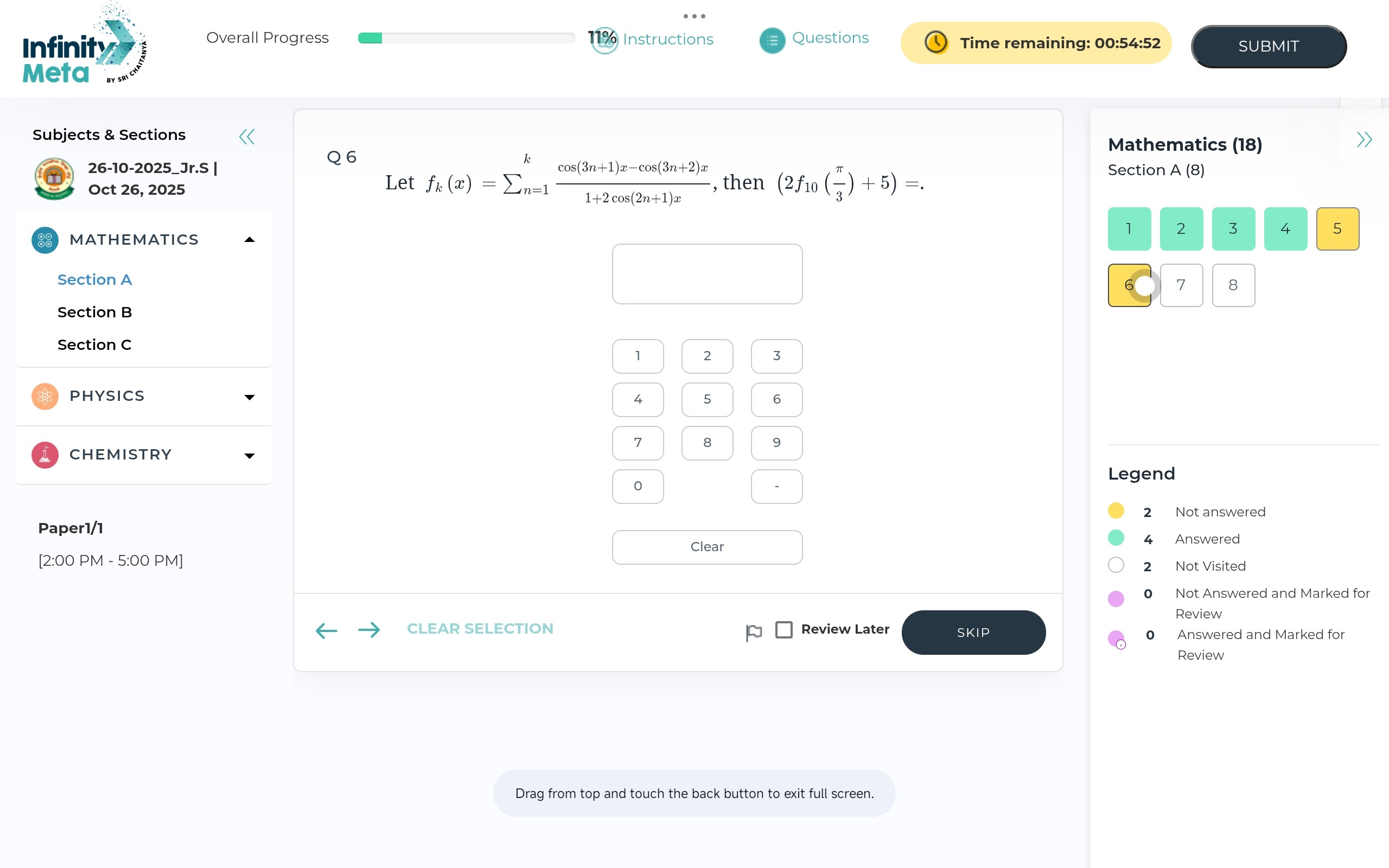
Let $f_k(x) = \sum_{n=1}^{k} \frac{\cos((3n+1)x) - \cos((3n+2)x)}{1+2\cos((2n+1)x)}$, then $(2f_{10}(\frac{\pi}{3})+5) =$.

• A. 5
• B. 10
• C. 0
• D. 1

Answer 1

Answer: (A)

5

Answer 2

The general term of the sum simplifies to $T_n(x) = 2 \sin(\frac{x}{2}) \sin(\frac{(2n+1)x}{2})$ using trigonometric identities. Evaluating at $x=\frac{\pi}{3}$, we get $T_n(\frac{\pi}{3}) = \sin(\frac{(2n+1)\pi}{6})$. The sequence of these terms for $n=1, 2, \dots$ is $1, \frac{1}{2}, -\frac{1}{2}, -1, -\frac{1}{2}, \frac{1}{2}$, which has a sum of 0 over every 6 terms. For $k=10$, $f_{10}(\frac{\pi}{3})$ is the sum of the first 10 terms. The sum of the first 6 terms is 0. The remaining terms are $T_7, T_8, T_9, T_{10}$, which are equal to $T_1, T_2, T_3, T_4$ respectively. So, $f_{10}(\frac{\pi}{3}) = 0 + 1 + \frac{1}{2} - \frac{1}{2} - 1 = 0$. Therefore, $2f_{10}(\frac{\pi}{3})+5 = 2(0)+5 = 5$.