Question
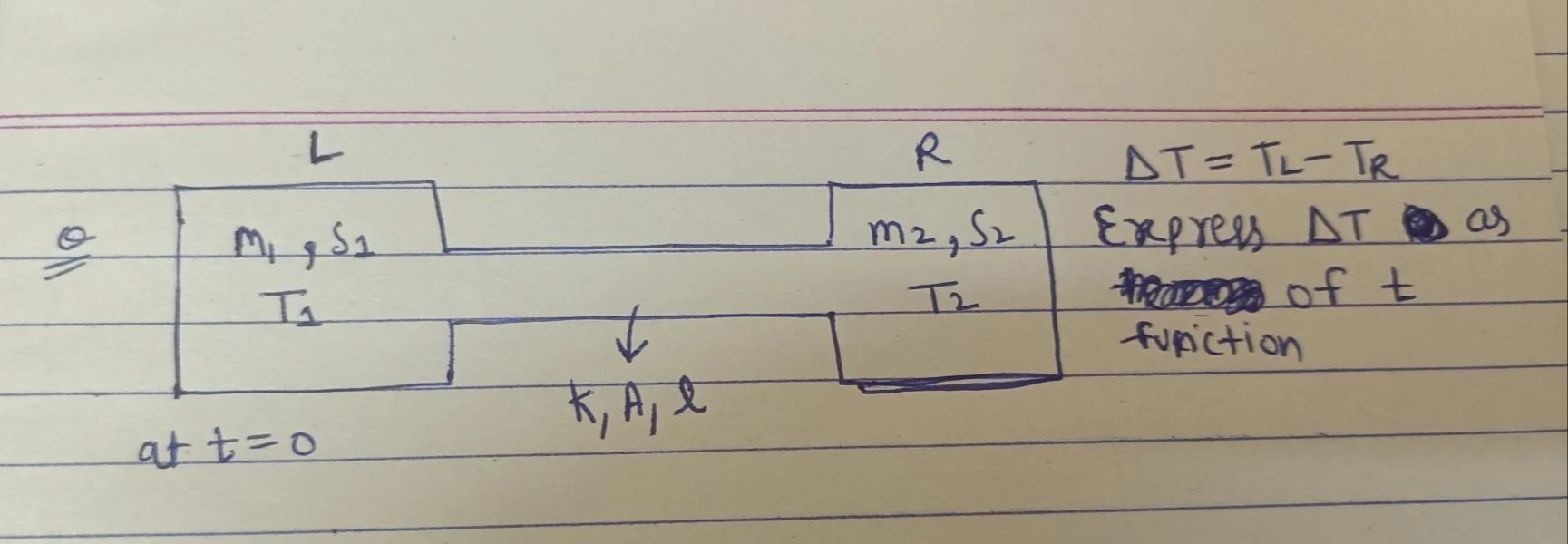
Question: L R △T=TL-TR m2, S2 Express Tas of t furiction 으 M₁, 51 Ti T2 ↓ K, A, l at t=0 ...
L R △T=TL-TR m2, S2 Express Tas of t furiction 으 M₁, 51 Ti T2 ↓ K, A, l at t=0
ΔT(t) = k e^(–δt)[C₁ cos(ω′t) + C₂ sin(ω′t)].
Solution
-
Setup:
– Write Newton’s second law for both blocks. Suppose the connecting section (spring) has spring‐constant k and that the difference in tensions (∆T = T₁–T₂) produces the restoring force on the effective mass of the system.
– Include frictional damping (if μ is the coefficient and g the gravitational acceleration) so that the net force on the system is
(m₁ + m₂) ẍ + μ(m₁ + m₂) g ẋ + k x = 0. -
Solution:
– Recognize that the above is the standard equation for a damped harmonic oscillator with
ω₀ = √(k/(m₁ + m₂)) and damping factor δ = μg/2.
– Hence the time–solution for displacement is
x(t) = e^(–δt)[C₁ cos(ω′t) + C₂ sin(ω′t)],
with ω′ = √(ω₀² – δ²) provided the motion is underdamped. -
Tension Difference Expression:
– Since the spring force (which equals the tension difference) is given by F = kx, we obtain
ΔT(t) = kx(t) = k e^(–δt)[C₁ cos(ω′t) + C₂ sin(ω′t)].
– The constants C₁ and C₂ are fixed from the initial conditions (e.g. the values of x(0) and ẋ(0)).
