Question

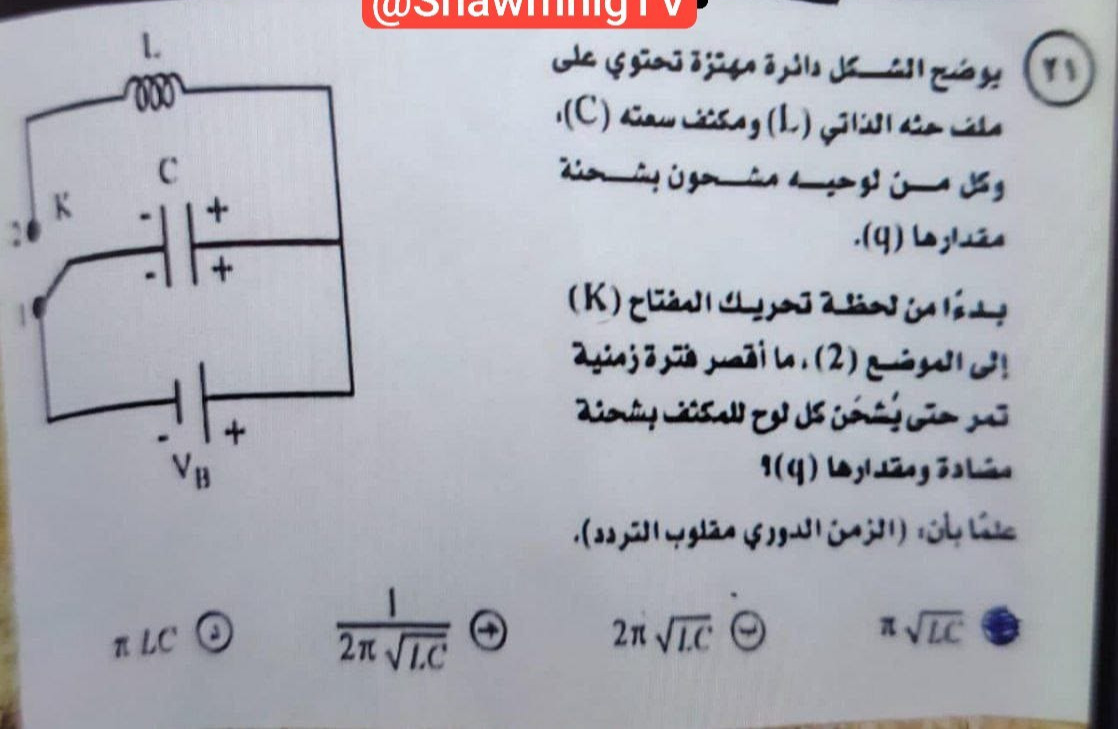
يوضح الشكل دائرة مهتزة تحتوي على ملف حثه الذاتي (L) ومكثف سعته (C) وكل من لوحيه مشحون بشحنة مقدارها (4).

بدءًا من لحظة تحريك المفتاح (K) إلى الموضع (2) ، ما أقصر فترة زمنية تمر حتى يشحن كل لوح للمكثف بشحنة مضادة ومقدارها (4) ؟

علما بأن الزمن الدوري مقلوب التردد).

• A. $\pi LC$
• B. $\frac{1}{2\pi \sqrt{L.C}}$
• C. $2\pi \sqrt{L.C}$
• D. $\pi \sqrt{L.C}$

Answer 1

Answer: (D)

$\pi \sqrt{L.C}$

Answer 2

The problem describes an LC oscillating circuit. Initially, the capacitor is charged with a charge of magnitude 'q'. When the switch K is moved to position 2, the charged capacitor is connected to the inductor, initiating LC oscillations.

The charge on the capacitor plates in an ideal LC circuit oscillates sinusoidally. If the initial charge at $t=0$ is $Q_0$, the charge $q(t)$ at any time $t$ can be described by:

$q(t) = Q_0 \cos(\omega t)$

where $Q_0$ is the maximum charge (which is 'q' in this problem) and $\omega$ is the angular frequency of the oscillation.

The angular frequency $\omega$ for an LC circuit is given by:

$\omega = \frac{1}{\sqrt{LC}}$

The time period of oscillation $T$ is related to $\omega$ by:

$T = \frac{2\pi}{\omega} = 2\pi\sqrt{LC}$

We are asked to find the shortest time until each plate of the capacitor is charged with an opposite charge of magnitude 'q'. This means we want the charge on the capacitor to become $-Q_0$.

So, we need to find the shortest time $t$ such that $q(t) = -Q_0$. Substituting this into the charge equation:

$-Q_0 = Q_0 \cos(\omega t)$ $-1 = \cos(\omega t)$

The smallest positive value of $\theta$ for which $\cos(\theta) = -1$ is $\theta = \pi$. Therefore, we set:

$\omega t = \pi$

Now, substitute the expression for $\omega$:

$\frac{1}{\sqrt{LC}} t = \pi$

Solving for $t$:

$t = \pi \sqrt{LC}$

This time corresponds to half a period of oscillation ($T/2$). At $t=0$, the capacitor has charge $Q_0$. At $t=T/4 = \frac{\pi\sqrt{LC}}{2}$, the capacitor is fully discharged ($q=0$). At $t=T/2 = \pi\sqrt{LC}$, the capacitor is fully charged again, but with the opposite polarity ($q=-Q_0$). This is exactly what the question asks for.