Question

If three reactions: A → Products Rate = K1[A]^X B → Products Rate = K2[B]^Y C → Products Rate = K3[C]^Z Value of $(\frac{X+Y}{4Z})$ is?

Answer 1

0.25

Answer 2

The given reactions are:

A → Products, Rate = $K_1 [A]^X$ B → Products, Rate = $K_2 [B]^Y$ C → Products, Rate = $K_3 [C]^Z$

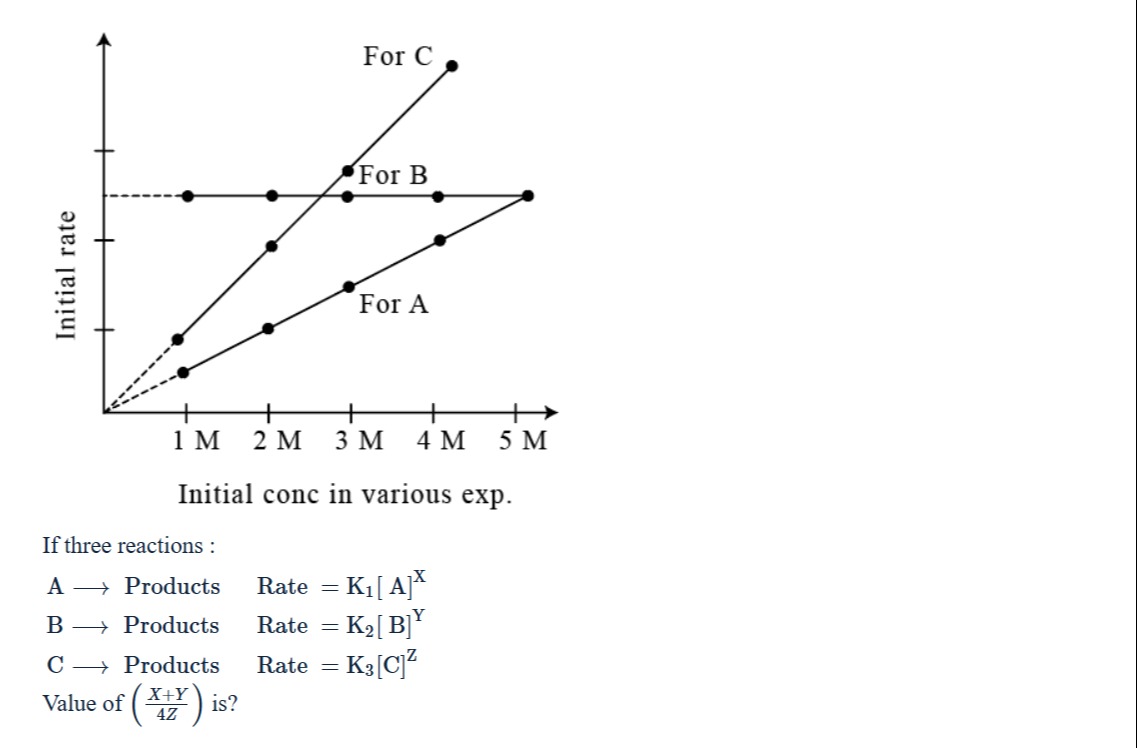
We need to determine the values of X, Y, and Z from the given graph, which plots the initial rate versus the initial concentration.

For reaction A: The graph for A is a straight line passing through the origin. This indicates that the initial rate is directly proportional to the initial concentration of A. The rate law is Rate = $K_1 [A]^X$. If the rate is directly proportional to [A], then $X=1$.

Let's verify this from the graph. Let the initial rate at [A] = 1 M be $R_0$. From the graph, it appears that the rate at [A] = 2 M is $2R_0$, at [A] = 3 M is $3R_0$, and at [A] = 4 M is $4R_0$. Substituting these values into the rate law: At [A] = 1 M, $R_0 = K_1 (1)^X$ At [A] = 2 M, $2R_0 = K_1 (2)^X$ Dividing the second equation by the first: $\frac{2R_0}{R_0} = \frac{K_1 (2)^X}{K_1 (1)^X}$, which simplifies to $2 = 2^X$. This gives $X = 1$. Thus, the order of reaction A with respect to A is $X = 1$.

For reaction B: The graph for B shows that the initial rate is constant for initial concentrations of B from 1 M to 4 M. The rate law is Rate = $K_2 [B]^Y$. If the rate is independent of the concentration of B, then $Y=0$. From the graph, the rate for B is constant at a certain value, which appears to be the same as the rate for A at [A] = 4 M, which is $4R_0$. So, Rate = $4R_0$ for [B] $\ge$ 1 M. Substituting into the rate law: $4R_0 = K_2 [B]^Y$. Since the rate is constant for different values of [B], the exponent Y must be 0. $4R_0 = K_2 [B]^0 = K_2$. Thus, the order of reaction B with respect to B is $Y = 0$.

For reaction C: The graph for C is a straight line passing through the origin. This indicates that the initial rate is directly proportional to the initial concentration of C raised to some power Z. Since it's a straight line through the origin on a linear plot, the power Z must be 1. The rate law is Rate = $K_3 [C]^Z$. Let's verify this from the graph. The line for C passes through the origin (0, 0). It also passes through the point where [C] = 2 M and the rate is the same as the rate for B, which is $4R_0$. So, at [C] = 2 M, Rate = $4R_0$. Substituting into the rate law: $4R_0 = K_3 (2)^Z$. Let's look at another point on the line for C. At [C] = 4 M, the rate appears to be $8R_0$ (twice the rate at [C] = 2 M, consistent with a linear relationship through the origin). So, at [C] = 4 M, Rate = $8R_0$. Substituting into the rate law: $8R_0 = K_3 (4)^Z$. We have two equations:

1. $4R_0 = K_3 2^Z$
2. $8R_0 = K_3 4^Z$ Dividing equation 2 by equation 1: $\frac{8R_0}{4R_0} = \frac{K_3 4^Z}{K_3 2^Z}$, which simplifies to $2 = \frac{4^Z}{2^Z} = \frac{(2^2)^Z}{2^Z} = \frac{2^{2Z}}{2^Z} = 2^{2Z-Z} = 2^Z$. So, $2 = 2^Z$, which gives $Z = 1$. Thus, the order of reaction C with respect to C is $Z = 1$.

We have found the values of X, Y, and Z: $X = 1$ $Y = 0$ $Z = 1$

We need to find the value of $(\frac{X+Y}{4Z})$. Substitute the values of X, Y, and Z into the expression: $(\frac{X+Y}{4Z}) = (\frac{1+0}{4 \times 1}) = (\frac{1}{4}) = 0.25$.

The final answer is $\boxed{0.25}$.

Explanation of the solution:

1. Analyze the graph for reaction A to determine the order X. The linear relationship through the origin indicates a first-order reaction, so X=1.
2. Analyze the graph for reaction B to determine the order Y. The constant rate for varying concentrations indicates a zero-order reaction, so Y=0.
3. Analyze the graph for reaction C to determine the order Z. The linear relationship through the origin indicates a first-order reaction, so Z=1.
4. Substitute the determined values of X, Y, and Z into the expression $(\frac{X+Y}{4Z})$ and calculate the result.