Question

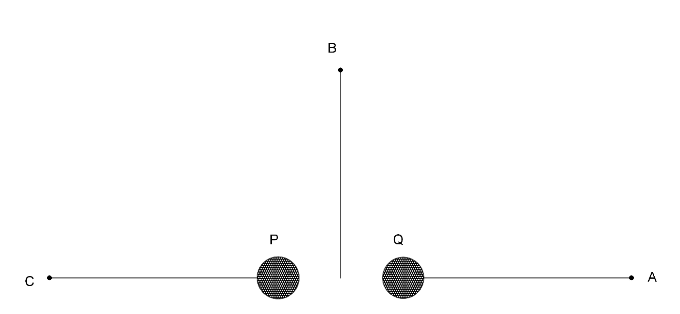
Figure here shows $P$ and $Q$ as two equally coherent sources emitting radiations of wavelength $20{\text{ }}m$. The separation $PQ$ is $5{\text{ }}m$ and the phase of $P$ is ahead of the phase of $Q$ by ${90^o}$. $A$, $B$ and $C$ are three distant points of observation equidistant from the midpoint of $PQ$. The intensity of radiations at $A$, $B$ and $C$ will bear the ratio

A. $0{\text{ }}:{\text{ }}1{\text{ }}:{\text{ }}4\:$
B. $4{\text{ }}:{\text{ }}1{\text{ }}:{\text{ }}0\:$
C. $0{\text{ }}:{\text{ }}1{\text{ }}:{\text{ }}2\:$
D. $2{\text{ }}:{\text{ }}1{\text{ }}:{\text{ }}0\:$

Answer 1

We will calculate the phase differences of each case from their path differences. Then, we will evaluate their net intensities. Finally, we will evaluate the ratio they bear.Two sources are said to be coherent when the waves emitted from them have the same frequency and constant phase difference.

Formulae Used:
$\Delta \phi {\text{ }} = {\text{ }}\dfrac{{2\pi }}{\lambda }{\text{ }}\Delta x$
${I_{Net}}{\text{ }} = {\text{ }}{I_1}{\text{ }} + {\text{ }}{I_2}{\text{ }} + {\text{ }}2\sqrt {{I_1}{I_2}} {\text{ }}\cos \theta$

Complete step by step answer:
The path difference for point $A$ can be written as,
$PA{\text{ }} - {\text{ }}QA$
We can clearly see that this refers to $PQ$,
Thus, we get
$\Delta {x_A}{\text{ }} = {\text{ }}PQ$
We are given in the question that,
$PQ{\text{ }} = {\text{ }}5{\text{ }}m$
Thus, we get
$\Delta {x_A}{\text{ }} = {\text{ }}5{\text{ }}m$
Now, phase difference at point $A$ is,
$\Delta {\phi _A}{\text{ }} = {\text{ }}\dfrac{{2\pi }}{\lambda }{\text{ }} \times {\text{ }}5$
Substituting $\lambda {\text{ }} = {\text{ }}20{\text{ }}m$, we get
$\Delta {\phi _A}{\text{ }} = {\text{ }}\dfrac{{2\pi }}{{20}}{\text{ }} \times {\text{ }}5$
After further evaluation, we get
$\Delta {\phi _A}{\text{ }} = {\text{ }}\dfrac{\pi }{2}$
Since, the distance between $Q$ and $A$ is less than that from $P$ and the phase difference is $\dfrac{\pi }{2}$.
Thus, we can say that the source wave from $Q$ will lead the wave from $P$.
But, we are given in the question that $P$ leads $Q$ by $\dfrac{\pi }{2}$.
Hence, net phase difference is,
$\Delta {\phi _{Ne{t_A}}}{\text{ }} = {\text{ }}\dfrac{\pi }{2}{\text{ }} - {\text{ }}\dfrac{\pi }{2}{\text{ }} = {\text{ }}0$

Now consider the intensities of $P$ and $Q$ be ${I_o}$
Thus, net intensity at $A$,
${I_A}{\text{ }} = {\text{ }}{I_o}{\text{ }} + {\text{ }}{I_o}{\text{ }} + {\text{ }}2\sqrt {{I_o}{\text{ }} \times {\text{ }}{I_o}} {\text{ }} \times {\text{ }}\cos {\text{ }}\left( {\Delta {\phi _{Ne{t_A}}}} \right)$
After substituting the values, we get
${I_A}{\text{ }} = {\text{ }}2{\text{ }}{I_o}{\text{ }} + {\text{ }}2\sqrt {{I_o}^2} {\text{ }} \times {\text{ }}\cos 0$
After calculations, we get
${I_A}{\text{ }} = {\text{ }}4{\text{ }}{I_o}$

Now, for the point $B$, waves from $P$ and $Q$ should travel equal distances.
Thus, the path difference is
$\Delta {x_B}{\text{ }} = {\text{ }}0$
Thus, phase difference at $B$
$\Delta {\phi _B}{\text{ }} = {\text{ }}0$
Thus, net phase difference is
$\Delta {\phi _{Ne{t_B}}}{\text{ }} = {\text{ }}\dfrac{\pi }{2}$
Thus, net intensity at $B$,
${I_B}{\text{ }} = {\text{ }}{I_o}{\text{ }} + {\text{ }}{I_o}{\text{ }} + {\text{ }}2\sqrt {{I_o}{\text{ }} \times {\text{ }}{I_o}} {\text{ }} \times {\text{ }}\cos {\text{ }}\left( {\Delta {\phi _{Ne{t_B}}}} \right)$

After substituting the values, we get
${I_B}{\text{ }} = {\text{ }}2{\text{ }}{I_o}{\text{ }} + {\text{ }}2\sqrt {{I_o}^2} {\text{ }} \times {\text{ }}\cos \dfrac{\pi }{2}$
After calculations, we get
${I_B}{\text{ }} = {\text{ }}2{\text{ }}{I_o}$
Again, the path difference for point $C$ can be written as,
$QC{\text{ }} - {\text{ }}PC$
We can clearly see that this refers to $PQ$,
Thus, we get
$\Delta {x_C}{\text{ }} = {\text{ }}PQ$
We are given in the question that,
$PQ{\text{ }} = {\text{ }}5{\text{ }}m$
Thus, we get
$\Delta {x_C}{\text{ }} = {\text{ }}5{\text{ }}m$

Now, phase difference at point $A$ is,
$\Delta {\phi _C}{\text{ }} = {\text{ }}\dfrac{{2\pi }}{\lambda }{\text{ }} \times {\text{ }}5$
Substituting $\lambda {\text{ }} = {\text{ }}20{\text{ }}m$, we get
$\Delta {\phi _C}{\text{ }} = {\text{ }}\dfrac{{2\pi }}{{20}}{\text{ }} \times {\text{ }}5$
After further evaluation, we get
$\Delta {\phi _C}{\text{ }} = {\text{ }}\dfrac{\pi }{2}$
Since, the distance between $P$ and $C$ is less than that from $Q$ and the phase difference is $\dfrac{\pi }{2}$. Thus, we can say that the source wave from $P$ will lead the wave from $Q$. But, we are given in the question that $P$ leads $Q$ by $\dfrac{\pi }{2}$.
Hence, net phase difference is,
$\Delta {\phi _{Ne{t_C}}}{\text{ }} = {\text{ }}\dfrac{\pi }{2}{\text{ }} + {\text{ }}\dfrac{\pi }{2}{\text{ }} = {\text{ }}\pi$
Thus, net intensity at $C$,
${I_C}{\text{ }} = {\text{ }}{I_o}{\text{ }} + {\text{ }}{I_o}{\text{ }} + {\text{ }}2\sqrt {{I_o}{\text{ }} \times {\text{ }}{I_o}} {\text{ }} \times {\text{ }}\cos {\text{ }}\left( {\Delta {\phi _{Ne{t_C}}}} \right)$

After substituting the values, we get
${I_C}{\text{ }} = {\text{ }}2{\text{ }}{I_o}{\text{ }} + {\text{ }}2\sqrt {{I_o}^2} {\text{ }} \times {\text{ }}\cos \pi$
After calculations, we get
${I_C}{\text{ }} = {\text{ }}0$
Hence,
The bearing ratio is
${I_A}{\text{ }}:{\text{ }}{I_B}{\text{ }}:{\text{ }}{I_C}{\text{ }} = {\text{ }}4{\text{ }}{I_o}{\text{ }}:{\text{ }}2{\text{ }}{I_o}{\text{ }}:{\text{ }}0$
Thus, we get
${I_A}{\text{ }}:{\text{ }}{I_B}{\text{ }}:{\text{ }}{I_C}{\text{ }} = {\text{ }}2{\text{ }}:{\text{ }}1{\text{ }}:{\text{ }}0$

Hence, the correct answer is D.

Note: Students should remember that the phase difference to be applied to the formula of intensity is the net phase difference and not the one for the particular case.Students often commit errors while substituting the value of trigonometric ratios. So they have to be very careful while doing so. Students often have a misconception that coherent sources have equal phase, intensities and frequencies but they should remember that coherent sources have equal intensities and frequencies while the phase may not be the same.