Question

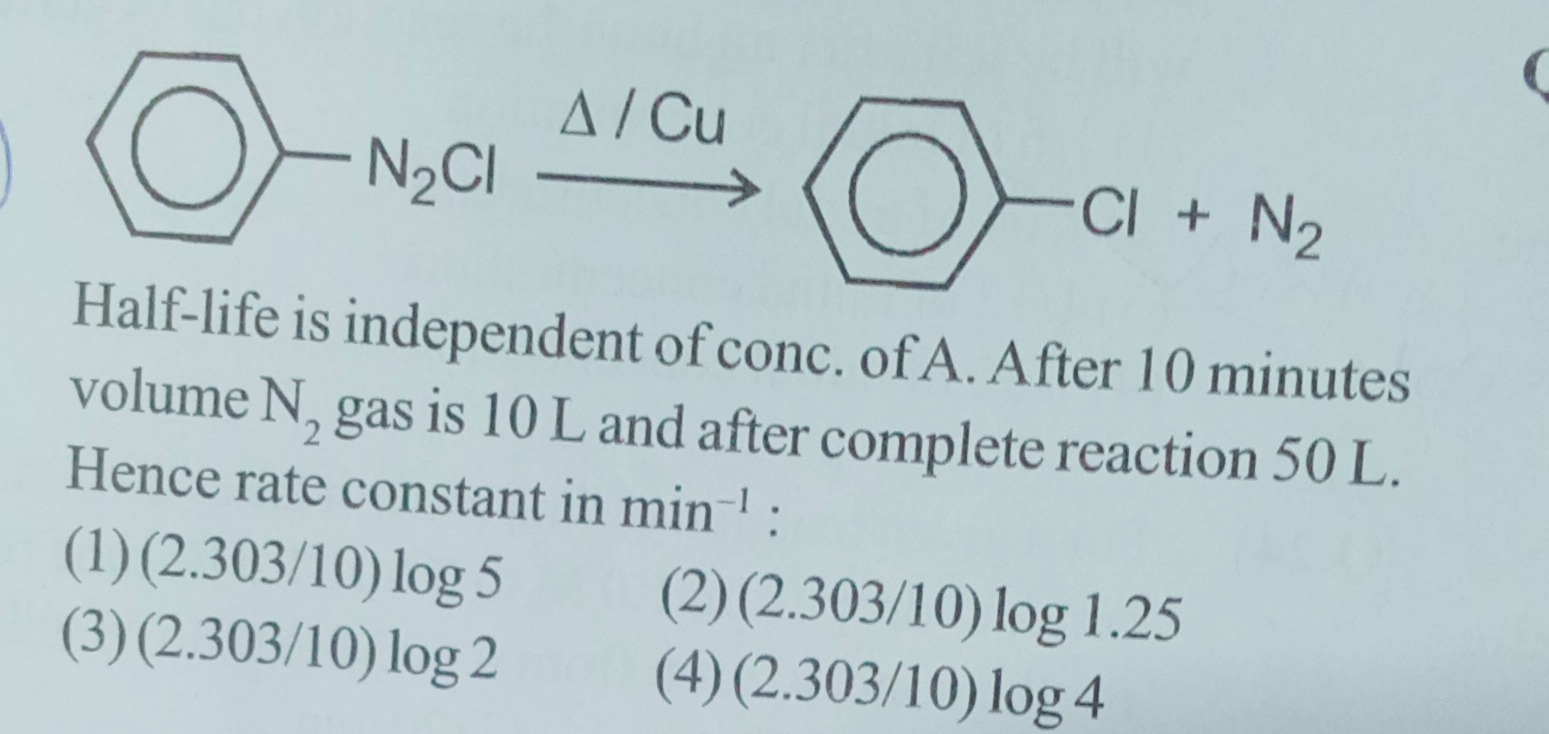
Half-life is independent of conc. of A. After 10 minutes volume N₂ gas is 10 L and after complete reaction 50 L. Hence rate constant in min⁻¹:

• A. (2.303/10) log 5
• B. (2.303/10) log 1.25
• C. (2.303/10) log 2
• D. (2.303/10) log 4

Answer 1

Answer: (B)

(2.303/10) log 1.25

Answer 2

The half-life of the reaction is independent of the concentration of reactant A, which means the reaction is a first-order reaction with respect to A. The reaction is the decomposition of benzene diazonium chloride ($\text{C}_6\text{H}_5\text{N}_2\text{Cl}$) to chlorobenzene ($\text{C}_6\text{H}_5\text{Cl}$) and nitrogen gas ($\text{N}_2$). The reaction is:

$\text{C}_6\text{H}_5\text{N}_2\text{Cl} \rightarrow \text{C}_6\text{H}_5\text{Cl} + \text{N}_2$

For a first-order reaction, the integrated rate law is given by:

$k = \frac{2.303}{t} \log \frac{[A]_0}{[A]_t}$

where $k$ is the rate constant, $t$ is the time, $[A]_0$ is the initial concentration of reactant A, and $[A]_t$ is the concentration of reactant A at time $t$.

In this reaction, nitrogen gas ($\text{N}_2$) is produced. The volume of $\text{N}_2$ gas produced is proportional to the amount of reactant A that has decomposed. Let $V_t$ be the volume of $\text{N}_2$ gas produced at time $t$, and $V_\infty$ be the volume of $\text{N}_2$ gas produced after the complete reaction.

The initial amount of reactant A is proportional to the total amount of $\text{N}_2$ that can be produced, which is proportional to $V_\infty$. So, $[A]_0 \propto V_\infty$.

The amount of reactant A that has reacted at time $t$ is proportional to the volume of $\text{N}_2$ produced at time $t$, which is $V_t$.

The amount of reactant A remaining at time $t$, $[A]_t$, is proportional to the initial amount minus the amount reacted. Thus, $[A]_t \propto V_\infty - V_t$.

Substituting these proportionalities into the first-order rate equation:

$k = \frac{2.303}{t} \log \frac{[A]_0}{[A]_t} = \frac{2.303}{t} \log \frac{V_\infty}{V_\infty - V_t}$

We are given:

Time $t = 10$ minutes.

Volume of $\text{N}_2$ gas at $t = 10$ minutes is $V_{10} = 10$ L.

Volume of $\text{N}_2$ gas after complete reaction is $V_\infty = 50$ L.

Substitute these values into the rate constant equation:

$k = \frac{2.303}{10} \log \frac{50}{50 - 10} = \frac{2.303}{10} \log \frac{50}{40} = \frac{2.303}{10} \log \frac{5}{4} = \frac{2.303}{10} \log 1.25$